Lab 10 Solution

Lab Instructor: Valeria Barra

Contents

Called Functions

DUE Tuesday 04-05-2016

Problem 1: Gaussian Quadrature

Use the transformation for your integrand 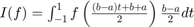$I(f) = \int_{-1}^{1} f \left( \frac{(b-a)t +b+a }{2} \right)\frac{b-a}{2} dt$ to approximate the Gaussian quadrature for n=2,4,6,8 for the functions:

$$(a) \int_1^2 \ln x dx=2 \ln 2 -1 \approx 0.38629436111989 $$

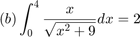
$$(b) \int_0^4 \frac{x}{\sqrt{x^2+9}} dx=2 $$

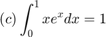
$$(c) \int_{0}^{1 } x e^x dx= 1 $$

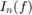$$(d) \int_{-1}^{2} x^5 dx = 10.5 $$ For each of the approximated integrals $I_n(f)$ calculate the error from the exact value of the integral $I(f)$, given by $Err_n=| I(f) - I_n(f) |$ and the Ratio $Ratio_n=\frac{Err_{n-1}}{Err_n}$ and put your results in tabular form

%*Solution*:
clear all; clc
format long e
% an array of lower endpoints of integration for all exercises
a = [1,  0, 0, -1];
% an array of upper endpoints of integration for all exercises
b = [2, 4, 1, 2];
% an array with the tranformation variables needed
c= (b-a)./2;

% an array exact solutions:
IExacts = [0.38629436111989,2,1,10.5];
% a vector with all n's for each exercise:
n = 2:2:8;

% an array of character strings to be diplayed in the table of results
Strings=['a' 'b' 'c' 'd'];
% all original functions handles in a cell-array
f={@(x) log(x), @(x) x./(sqrt(9 + x.^2)), @(x) x.*exp(x),@(x) x.^5};

for i=1:length(a)
    % first define another function handle cell-array with the proper tranformation
    F{i} =@(t) c(i)*f{i}((b(i)+a(i) + t.*(b(i)-a(i)))./2);
    fprintf('____________________________________________\n \n')
    disp(['Execution of part (',Strings(i),') f = ',char(f{i})])
    fprintf('____________________________________________\n')
    fprintf('\n Exact solution of part (%s) = %f \n \n ',Strings(i),IExacts(i))
    fprintf('\n  n     Gaussian Quadrature      Error_n  \n')
    fprintf('____________________________________________\n')
    for j = 1 : length(n)
        % calculate and print results
        In(j)=Gaussian(F{i},n(j));
        Err(j)=abs(IExacts(i)- Gaussian(F{i},n(j)));
        fprintf(' %2i  %20.8e  %15.6e \n',n(j),In(j),Err(j));
    end
    fprintf('____________________________________________\n \n \n')
end

____________________________________________
 
Execution of part (a) f = @(x)log(x)
____________________________________________

 Exact solution of part (a) = 0.386294 
 
 
  n     Gaussian Quadrature      Error_n  
____________________________________________
  2        3.86594944e-01     3.005830e-04 
  4        3.86294497e-01     1.358196e-07 
  6        3.86294361e-01     7.870166e-11 
  8        3.86294361e-01     3.852452e-11 
____________________________________________
 
 
____________________________________________
 
Execution of part (b) f = @(x)x./(sqrt(9+x.^2))
____________________________________________

 Exact solution of part (b) = 2.000000 
 
 
  n     Gaussian Quadrature      Error_n  
____________________________________________
  2        1.99171503e+00     8.284971e-03 
  4        2.00004093e+00     4.093368e-05 
  6        1.99999995e+00     4.865641e-08 
  8        2.00000000e+00     3.578167e-10 
____________________________________________
 
 
____________________________________________
 
Execution of part (c) f = @(x)x.*exp(x)
____________________________________________

 Exact solution of part (c) = 1.000000 
 
 
  n     Gaussian Quadrature      Error_n  
____________________________________________
  2        9.98257837e-01     1.742163e-03 
  4        9.99999992e-01     7.948769e-09 
  6        1.00000000e+00     9.370282e-12 
  8        1.00000000e+00     1.014595e-10 
____________________________________________
 
 
____________________________________________
 
Execution of part (d) f = @(x)x.^5
____________________________________________

 Exact solution of part (d) = 10.500000 
 
 
  n     Gaussian Quadrature      Error_n  
____________________________________________
  2        7.12500000e+00     3.375000e+00 
  4        1.05000000e+01     6.145147e-10 
  6        1.05000000e+01     8.833005e-10 
  8        1.05000000e+01     1.092573e-09 
____________________________________________

Comments on Results:

We can see that for each execution of the code the error decreases as n increases. Generally Gaussian quadrature is better than other integration rules seen in the previous assignment (Trapezoid or Simpson rules). The degree of precision of a quadrature method is the degree for which all polynomial functions are integrated by the method with no error. In this case, you can see it from the polynomial function in ex. (d) of degree 5 (n+1 with n=4), the Gaussian quadrature with four points is already exact up to the 9th digit.


Published with MATLAB® R2015a

Gaussian
function [I] = Gaussian( f,n)

% we need to discern the cases for each n to set the proper nodes and weights
switch n
   case 2
       x= [-0.5773502692,0.5773502692];
       w= [1,1];
   case 4
       x= [-0.8611363116,-0.3399810436,0.3399810436,0.8611363116];
       w= [0.3478548451,0.6521451549,0.6521451549,0.3478548451];
   case 6
       x= [-0.9324695142,-0.6612093865,-0.2386191861,0.2386191861,0.6612093865,0.9324695142];
       w= [0.1713244924,0.3607615730,0.4679139346,0.4679139346,0.3607615730,0.1713244924];
   case 8
       x= [-0.9602898565,-0.7966664774,-0.5255324099,-0.1834346425,0.1834346425,0.5255324099,0.7966664774,0.9602898565];
       w= [0.1012285363,0.2223810345,0.3137066459,0.3626837834,0.3626837834,0.3137066459,0.2223810345,0.1012285363];
   otherwise
       disp('You need to use n 2,4,6 or 8');
       out=0;
end
I=0;
for i=1:n
    I=I + w(i)*f(x(i));
end
end


Published with MATLAB® R2015a