Lab 9 Solution

Lab Instructor: Valeria Barra

Contents

Called Functions

DUE Tuesday 03-29-2016

Problem 1: Numerical Integration: Trapezoid Rule and Simpson's rule

Use Trapezoid Method and Simpson's Method to find the approximations 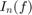$I_n(f)$ of integrals 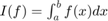$I(f)=\int_a^b f(x)dx$, with 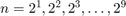$n=2^1, 2^2, 2^3, \ldots , 2^9$, for the functions:

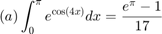
$$ (a) \int_0^\pi e^{\cos(4x)} dx=\frac{e^{\pi} -1}{17} $$

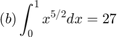
$$(b) \int_0^1 x^{5/2} dx= {2}{7} $$

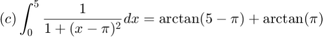
$$(c) \int_0^5 \frac{1}{1+(x-\pi)^2} dx= \arctan(5 - \pi)+ \arctan(\pi) $$

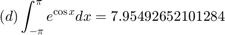
$$(d) \int_{-\pi}^{\pi } e^{\cos x} dx= 7.95492652101284 $$

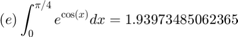
$$(e) \int_0^{\pi/4} e^{\cos(x)} dx = 1.93973485062365 $$

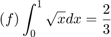
$$(f) \int_0^1 \sqrt{x} dx =\frac{2}{3} \\$$

For each of the approximated integrals 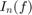$I_n(f)$ calculate the error from the exact value of the integral 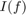$I(f)$, given by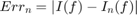 $Err_n=| I(f) - I_n(f) |$

Solution:

clear all; clc;
format long e
% all functions handles in a cell array
f = {@(x) exp(x).*cos(4.*x), @(x)(x.^(5/2)), @(x) 1./(1+(x-pi).^2), @(x) exp(cos(x)), @(x) exp(cos(x)), @(x) sqrt(x)};
% an array of lower endpoints of integration for all exercises
a = [0, 0, 0, -pi, 0, 0];
% an array of upper endpoints of integration for all exercises
b = [pi, 1, 5,  pi, pi/4, 1];
% an array exact solutions:
I = [(exp(pi) -1)/17,2/7,atan(pi - 5) + atan(pi), 7.95492652101284,1.93973485062365,2/3];
% a vector with all n's for each exercise:
n = 2.^(1:9);

% an array of character strings to be diplayed in the table of results
Strings=['a' 'b' 'c' 'd' 'e' 'f'];

% we will call the three methods Trapezoid, Simpson's and Midpoint in a
% nested loop. One loop goes over each single exercise ((a) to (f)); one
% for each of them goes over all the n's
for i=1:length(a)
    fprintf('Execution of part (%s) \n',Strings(i))
    fprintf('  n       Trap Rule         Error_n Trap       Ratio_n Trap     Simpson''s Rule    Error_n Simps      Ratio_n Simps\n')
    fprintf('===============================================================================================================================\n')
    for j = 1:length(n)
        Tr = Trapezoid(f{i},a(i),b(i),n(j));
        S = Simpson(f{i},a(i),b(i),n(j));
        ErrTrap(j)=abs(I(i)- Tr);
        ErrSimps(j)=abs(I(i)- S);
        if j<2
            fprintf('%3i  %15.8f    %15.8f    %15s   %15.8f   %15.8f   %15s \n', n(j),Tr,ErrTrap(j),'',S,ErrSimps(j),'')
        else
            RatioTrap(j-1)=ErrTrap(j-1)/ErrTrap(j);
            RatioSimps(j-1)=ErrSimps(j-1)/ErrSimps(j);
            fprintf('%3i  %15.8f    %15.8f    %15.8f   %15.8f   %15.8f   %15.8f  \n', n(j),Tr,ErrTrap(j),RatioTrap(j-1),S,ErrSimps(j),RatioSimps(j-1))
        end
    end
    % end of each table
 fprintf('===============================================================================================================================\n')
end

Execution of part (a) 
  n       Trap Rule         Error_n Trap       Ratio_n Trap     Simpson's Rule    Error_n Simps      Ratio_n Simps
===============================================================================================================================
  2      26.51633586        25.21394217                          22.71507737       21.41268369                   
  4       3.24905049         1.94665681        12.95243314       -4.50671129        5.80910498        3.68605556  
  8       1.62452525         0.32213156         6.04304897        1.08301683        0.21937685       26.48002697  
 16       1.37572252         0.07332883         4.39297270        1.29278827        0.00960541       22.83888525  
 32       1.32031188         0.01791819         4.09242320        1.30184167        0.00055202       17.40050791  
 64       1.30684789         0.00445420         4.02276262        1.30235989        0.00003380       16.33364836  
128       1.30350566         0.00111197         4.00566951        1.30239158        0.00000210       16.08242503  
256       1.30267158         0.00027790         4.00141606        1.30239355        0.00000013       16.02052283  
512       1.30246315         0.00006947         4.00035389        1.30239368        0.00000001       16.00662328  
===============================================================================================================================
Execution of part (b) 
  n       Trap Rule         Error_n Trap       Ratio_n Trap     Simpson's Rule    Error_n Simps      Ratio_n Simps
===============================================================================================================================
  2       0.33838835         0.05267406                           0.28451780        0.00119649                   
  4       0.29879150         0.01307721         4.02792796        0.28559255        0.00012174        9.82823468  
  8       0.28897474         0.00326045         4.01085576        0.28570249        0.00001180       10.31849208  
 16       0.28652857         0.00081428         4.00408363        0.28571318        0.00000111       10.64428802  
 32       0.28591778         0.00020349         4.00150493        0.28571418        0.00000010       10.85810433  
 64       0.28576515         0.00005087         4.00054731        0.28571428        0.00000001       11.00024432  
128       0.28572700         0.00001272         4.00019730        0.28571428        0.00000000       11.09627668  
256       0.28571746         0.00000318         4.00007071        0.28571429        0.00000000       11.16201052  
512       0.28571508         0.00000079         4.00002524        0.28571429        0.00000000       11.20714250  
===============================================================================================================================
Execution of part (c) 
  n       Trap Rule         Error_n Trap       Ratio_n Trap     Simpson's Rule    Error_n Simps      Ratio_n Simps
===============================================================================================================================
  2       2.16665484         1.98116662                           2.62509546        2.43960723                   
  4       2.26866764         2.08317942         0.95103024        2.30267191        2.11718368        1.15228889  
  8       2.33227047         2.14678224         0.97037295        2.35347141        2.16798318        0.97656832  
 16       2.33781288         2.15232465         0.99742492        2.33966035        2.15417213        1.00641130  
 32       2.33927712         2.15378890         0.99932016        2.33976520        2.15427698        0.99995133  
 64       2.33964394         2.15415572         0.99982972        2.33976622        2.15427799        0.99999953  
128       2.33973570         2.15424747         0.99995741        2.33976628        2.15427805        0.99999997  
256       2.33975864         2.15427041         0.99998935        2.33976628        2.15427806        1.00000000  
512       2.33976437         2.15427614         0.99999734        2.33976628        2.15427806        1.00000000  
===============================================================================================================================
Execution of part (d) 
  n       Trap Rule         Error_n Trap       Ratio_n Trap     Simpson's Rule    Error_n Simps      Ratio_n Simps
===============================================================================================================================
  2       9.69546157         1.74053505                          12.15679720        4.20187068                   
  4       7.98932344         0.03439692        50.60148152        7.42061073        0.53431579        7.86402112  
  8       7.95492777         0.00000125     27480.40488126        7.94346255        0.01146397       46.60826574  
 16       7.95492652         0.00000000    234879409.83333334        7.95492610        0.00000042    27476.40521271  
 32       7.95492652         0.00000000         1.00000000        7.95492652        0.00000000   93951762.80000000  
 64       7.95492652         0.00000000         1.00000000        7.95492652        0.00000000        0.83333333  
128       7.95492652         0.00000000         0.60000000        7.95492652        0.00000000        1.00000000  
256       7.95492652         0.00000000         1.66666667        7.95492652        0.00000000        3.00000000  
512       7.95492652         0.00000000         0.28571429        7.95492652        0.00000000        0.11111111  
===============================================================================================================================
Execution of part (e) 
  n       Trap Rule         Error_n Trap       Ratio_n Trap     Simpson's Rule    Error_n Simps      Ratio_n Simps
===============================================================================================================================
  2       1.92117917         0.01855568                           1.94027033        0.00053548                   
  4       1.93511966         0.00461519         4.02056590        1.93976649        0.00003164       16.92502346  
  8       1.93858251         0.00115234         4.00507489        1.93973680        0.00000195       16.23047908  
 16       1.93944686         0.00028799         4.00126462        1.93973497        0.00000012       16.05704615  
 32       1.93966286         0.00007199         4.00031590        1.93973486        0.00000001       16.01422667  
 64       1.93971685         0.00001800         4.00007896        1.93973485        0.00000000       16.00359065  
128       1.93973035         0.00000450         4.00001974        1.93973485        0.00000000       16.00100507  
256       1.93973373         0.00000112         4.00000493        1.93973485        0.00000000       16.02066811  
512       1.93973457         0.00000028         4.00000118        1.93973485        0.00000000       16.06563707  
===============================================================================================================================
Execution of part (f) 
  n       Trap Rule         Error_n Trap       Ratio_n Trap     Simpson's Rule    Error_n Simps      Ratio_n Simps
===============================================================================================================================
  2       0.60355339         0.06311328                           0.63807119        0.02859548                   
  4       0.64328305         0.02338362         2.69903783        0.65652626        0.01014040        2.81995522  
  8       0.65813022         0.00853645         2.73926913        0.66307928        0.00358739        2.82668222  
 16       0.66358120         0.00308547         2.76665974        0.66539819        0.00126848        2.82810303  
 32       0.66555894         0.00110773         2.78539780        0.66621818        0.00044848        2.82836905  
 64       0.66627081         0.00039586         2.79832156        0.66650810        0.00015856        2.82841682  
128       0.66652566         0.00014101         2.80729776        0.66661061        0.00005606        2.82842530  
256       0.66661655         0.00005012         2.81356482        0.66664685        0.00001982        2.82842680  
512       0.66664888         0.00001779         2.81795678        0.66665966        0.00000701        2.82842707  
===============================================================================================================================

Conclusions:

Problem 2

Solution: To solve this problem, we need to test monomial functions 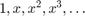$1, x, x^2, x^3,\ldots$ on a general interval [a,b]=[x,x+4h], where both x and h are symbolic variables. Note that we apply to all integration rules the same number of points 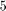$5$, since Boole's rule needs at least this number of nodes. But the results would be unchanged, even if we tested Trapezoid and Simpson's rules with fewer nodes.

n = 5;
syms x h;
monomials = sym(zeros(1, n));

for k=0:n+1
    monomials(k+1) = sym(x^k);
    Real(k+1)= collect((( x + 4*h)^(k+1)  - x^(k+1) )/(k+1),h);
end


for k=0:n+1
    T=collect(TrapezoidSym(monomials(k+1),x,x+4*h,h,n),h);
    testT=isequal(T,Real(k+1));
    if (testT==0)
        fprintf('The order of precision for Trapezoid is is %d\n',k-1)
        break
    end
end

for k=0:n+1
    S=collect(SimpsonSym(monomials(k+1),x,x+4*h,h,n),h);
    testS=isequal(S,Real(k+1));
    if (testS==0)
        fprintf('The order of precision for Simpson is is %d\n',k-1)
        break
    end
end

for k=0:n+1
    B=collect(Boole(monomials(k+1),x,x+4*h,h,n),h);
    testB=isequal(B,Real(k+1));
    if (testB==0)
        fprintf('The order of precision for Boole''s is %d\n',k-1)
        break
    end
end

The order of precision for Trapezoid is is 1
The order of precision for Simpson is is 3
The order of precision for Boole's is 5


Published with MATLAB® R2015a

Boole
function B=Boole(f,x,b,h,n)
B=0;

for i=1:n-2
    if mod(i,2)==0 % if i is even we multiply the corresponding coefficient in the summation
        B=B+12*subs(f,x+i*h);
    else % else, i is odd
        B=B+32*subs(f,x+i*h);
    end
end
B=((2*h)/45)*(7*subs(f,x)+B+7*subs(f,b)); % calculate the summation considering the first and the last cases separate
end


Published with MATLAB® R2015a

Simpson
function S=Simpson(f,a,b,n)
h=(b-a)/n;
S=0;
x=a; % initialize x as the first grid point
for i=1:n-1
    x=x+h;  % this way we create the equispaced grid everytime adding h
    if mod(i,2)==0 % if i is even we multiply the corresponding coefficient in the summation
        S=S+2*f(x);
    else % else, i is odd
        S=S+4*f(x);
    end
end
S=(h/3)*(f(a)+S+f(b)); % calculate the summation considering the first and the last cases separate
end


Published with MATLAB® R2015a

SimpsonSym
function S=SimpsonSym(f,x,b,h,n)
S=0;
for i=1:n-2
    if mod(i,2)==0 % if i is even we multiply the corresponding coefficient in the summation
        S=S+2*subs(f,x+i*h);
    else % else, i is odd
        S=S+4*subs(f,x+i*h);
    end
end
S=(h/3)*(subs(f,x)+S+subs(f,b)); % calculate the summation considering the first and the last cases separate
end


Published with MATLAB® R2015a

Trapezoid
function T = Trapezoid(f,a,b,n)
    h = (b-a)/n;
    S = 0;
    x = a; % initialize x as the first grid point
    for i = 1:n-1
        x = x + h; % this way we create the equispaced grid everytime adding h
        S = S + f(x); % calculate the summation S of the internal grid points only
    end
    T = h*(0.5*f(a) + S + 0.5*f(b)); % calculate the summation considering the first and the last cases separate
end


Published with MATLAB® R2015a

TrapezoidSym
function T = TrapezoidSym(f,x,b,h,n)
    S = 0;
    for i = 1:n-2
        S = S + subs(f,x+i*h); % calculate the summation S of the internal grid points only
    end
    T = h*(0.5*subs(f,x) + S + 0.5*subs(f,b)); % calculate the summation considering the first and the last cases separate
end


Published with MATLAB® R2015a