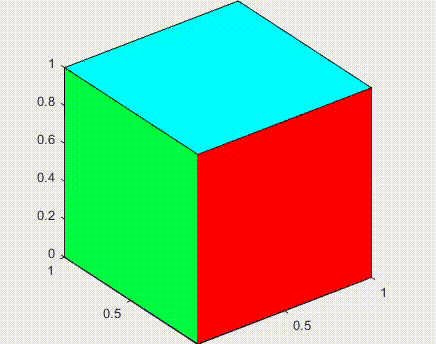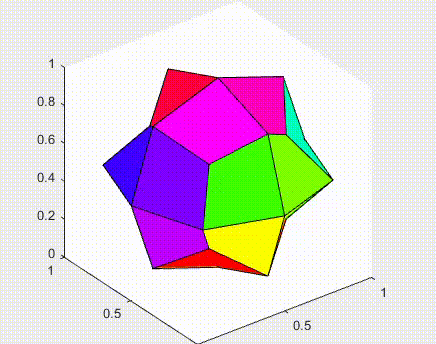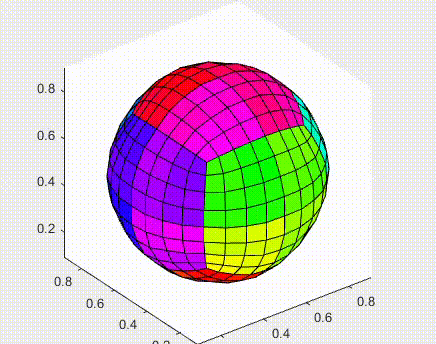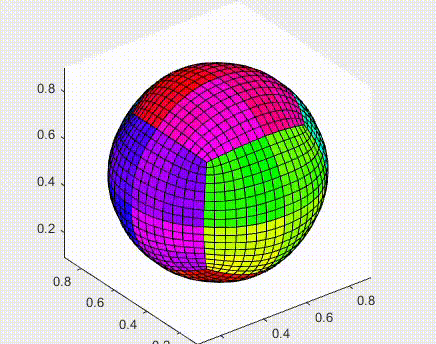
Implemented the original algorithm by Catmull-Clark for closed surfaces. The phrase subdivision surfaces, in the field of 3D Computer Graphics, refers to a class of surfaces that are obtained with the aid of computers through repeated refinements of their control points polyhedra. The Catmull-Clark subdivision algorithm works on polyhedra with arbitrary topology, and the limit-surface generated is a uniform bicubic B-spline surface of class C², except at points that have a number of adjacent edges different from four, called extraordinary points, where they have C¹ continuity.

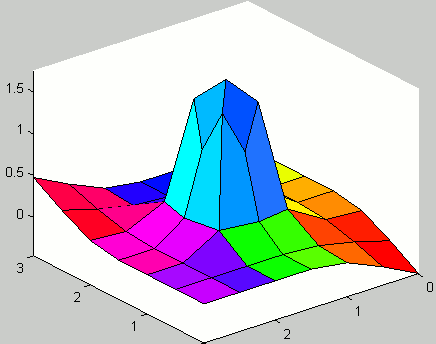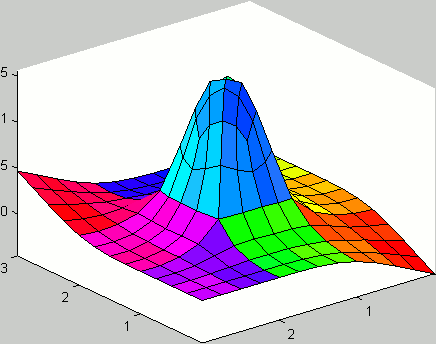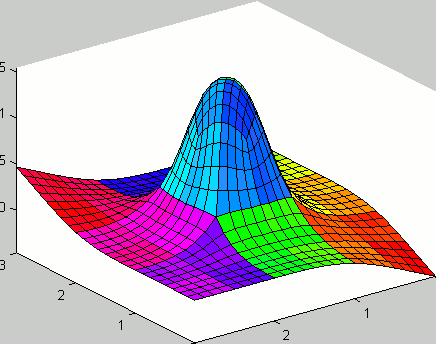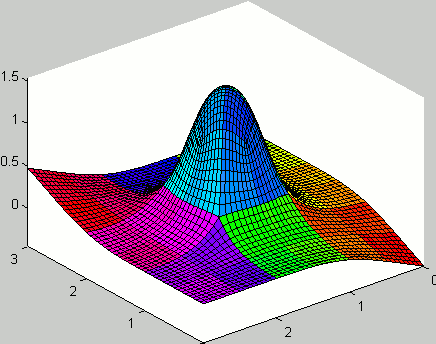
Expanded the original algorithm, that only accounted for closed surfaces, to include open surfaces. In this case, the boundary conditions were considered following the approach by Nasri (i.e. the auxiliary ghost nodes were found by linear extrapolations of the internal nodes).

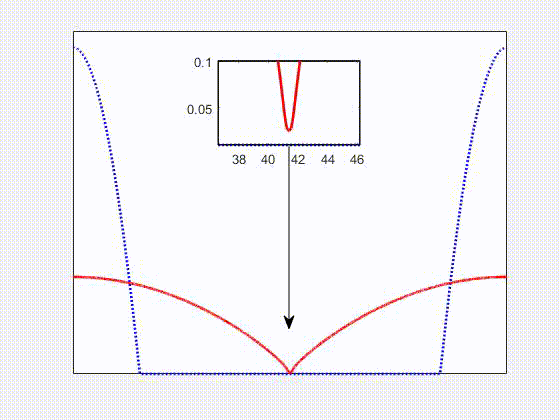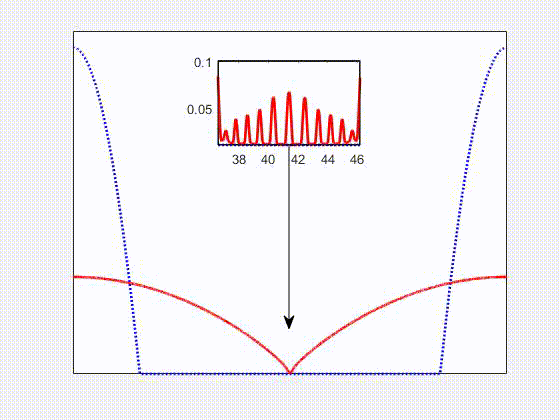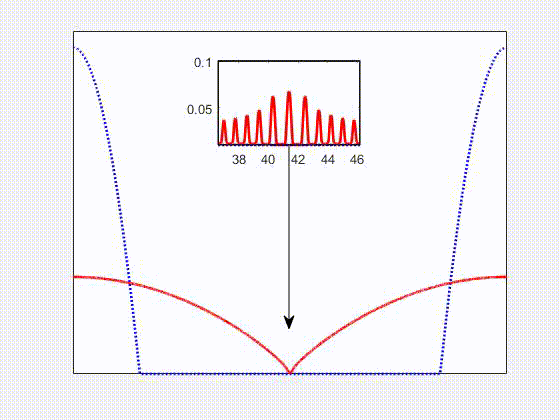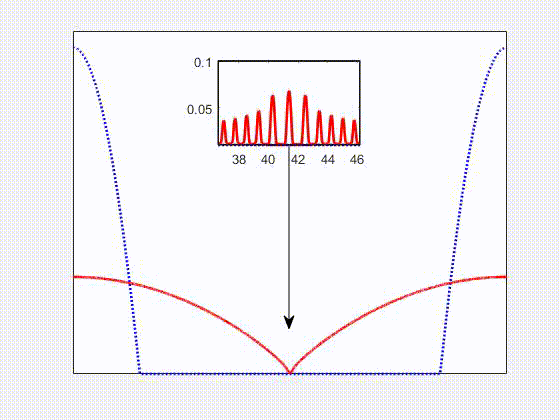
Carried out a computational investigation, in the field of Computational Fluid Dynamics, for thin viscoelastic films on a flat solid substrate subject to the van der Waals interaction force. The governing equations are obtained within a thin film approximation of the Navier-Stokes equations with Jeffreys model for viscoelastic stresses. The resulting equation is a second order in time and fourth order in space Partial Differential Equation. The numerical method chosen is an implicit finite difference scheme, with adaptive time step discretization and fixed grid size. The investigation focused on the effects of non-Newtonian viscoelasticity, Newtonian viscosity, and the substrate slippage on the dynamics of thin viscoelastic films. This work is part of my PhD thesis project, developed within the Complex Flows and Soft Matter Group, and it has been published in V. Barra, S. Afkhami, L. Kondic, Interfacial dynamics of thin viscoelastic films and drops, Journal of Non-Newtonian Fluid Mechanics, 237, 26-38 (2016)

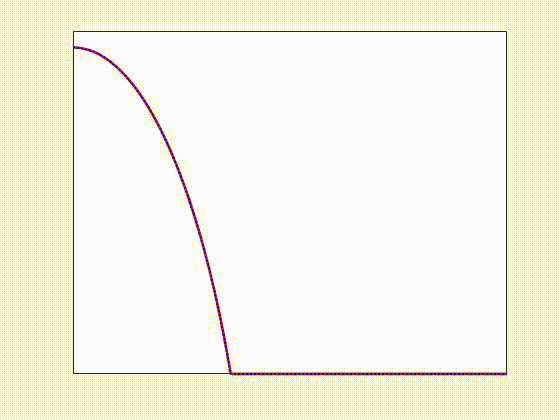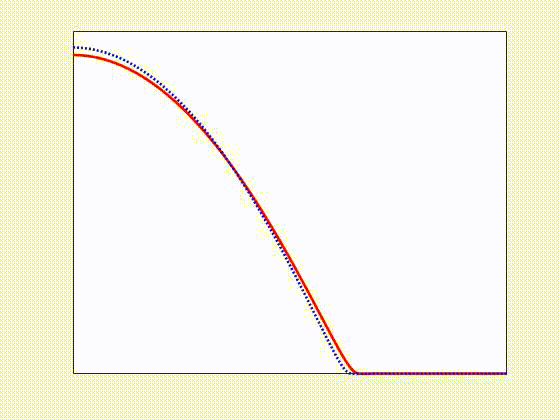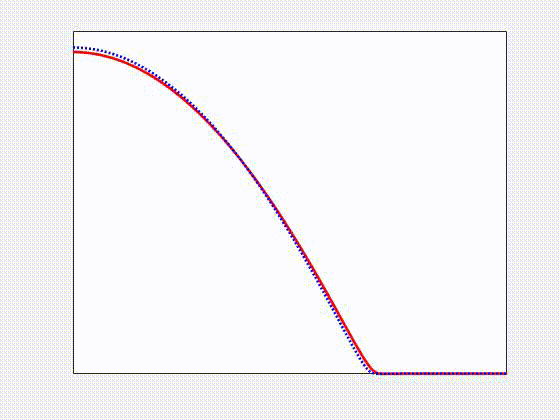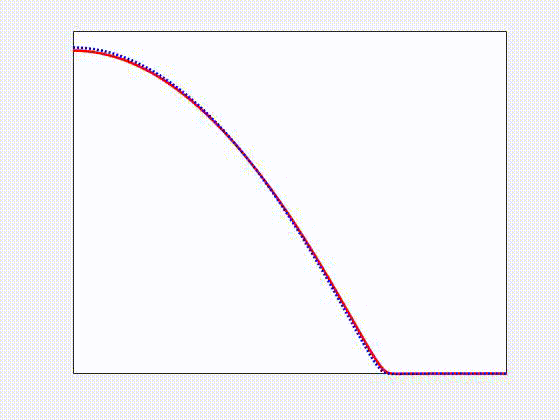
Numerical simulations of a spreading non-Newtonian viscoelastic drop (red solid) compared to a Newtonian one (blue dotted) on a flat solid substrate. We found that elastic effects lead to deviations from the Cox-Voinov law for partially wetting fluids. In general, elastic effects enhance spreading, and suppress retraction, compared to Newtonian ones. This work is part of my PhD thesis project, developed within the Complex Flows and Soft Matter Group, and it has been published in V. Barra, S. Afkhami, L. Kondic, Interfacial dynamics of thin viscoelastic films and drops, Journal of Non-Newtonian Fluid Mechanics, 237, 26-38 (2016)

Numerical simulations of the dynamics of free-boundary flows of viscoelastic liquid membranes. The governing equation describes the balance of linear momentum, in which the stresses include the viscoelastic response to deformations of Maxwell type. A penalty method is utilized to enforce near incompressibility of the viscoelastic media, and a finite element method is used, in which the slender geometry representing the liquid membrane is discretized by linear three-node triangular elements under plane stress conditions. The video shows the numerical solution of a sheared Cook's membrane of Maxwell type. This work is part of my PhD thesis project, developed within the Complex Flows and Soft Matter Group, and it has been published in V. Barra, S. A. Chester, S. Afkhami, Numerical Simulations of Nearly Incompressible Viscoelastic Membranes, Computers and Fluids, 175, 36-47 (2018)

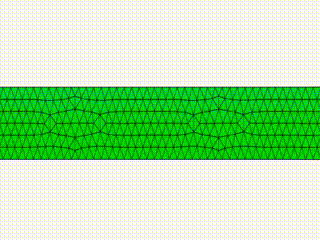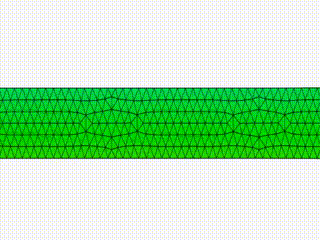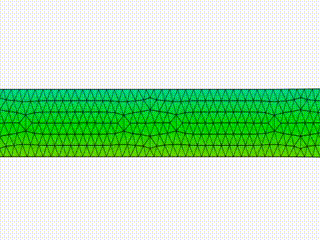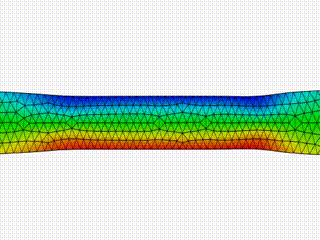
The video shows the numerical solution of the drawing of a viscoelastic membrane with constant thickness, as a planar study of a more general redrawing process of viscoelastic sheets. Drawing or redrawing processes are manufacturing practices for which a sheet, usually of glass or metal, is heated and stretched to obtain a reduced cross sectional area, such as in the production of glass fibers. This work is part of my PhD thesis project, developed within the Complex Flows and Soft Matter Group, and it has been published in V. Barra, S. A. Chester, S. Afkhami, Numerical Simulations of Nearly Incompressible Viscoelastic Membranes, Computers and Fluids, 237, 26-38 (2016)

Interned in the Research group at Pixar Animation Studios. Developed a proprietary C++ library for a 2D Navier-Stokes solver for viscous fluid simulations on surfaces with arbitrary curvature. Expanded existing code to include different types of discretized domains (from triangular to polygonal meshes). Included user-defined solid obstacle and boundary conditions for open meshes. Prototyped the development of a plug-in for third-party procedural 3D animation and special effects software for film and entertainment, Houdini by SideFX. Developed a proprietary C++ library to simulate the dynamics and interface instabilities of 3D thin viscous films on triangular surfaces with arbitrary curvature.