Cleverness With Light

We said that stars are just tiny points of light, yet we can tell many things about stars.  We can tell

• what they are made of,
• how hot they are,
• how big they are (their radius),
• how fast they rotate,
• whether they are expanding or contracting,
• ...and many other things (like their masses, whether they have planets, etc.).

How can we do all of this?  It is by being clever with light -- by understanding everything we can about how light works, how it interacts with matter, etc.  We already learned how to do several of the things in the above list.  For example, we use spectral lines to determine what stars are made of.  We use the continuum spectrum (or the star's color) to determine how hot they are.  We use doppler shifts of spectral lines to determine whether they are expanding or contracting, and "doppler broadening" to determine how fast they rotate.

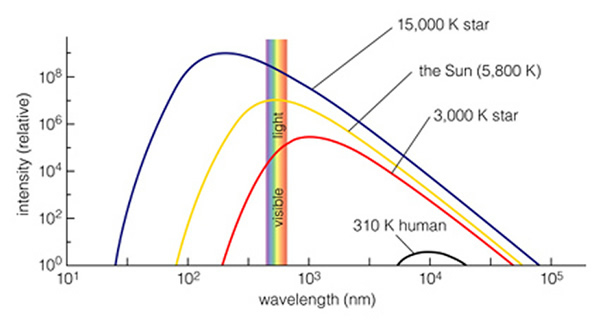
What we have not talked about yet is how to tell how big they are.  This is a very important point, but it takes a couple of steps we haven't learned yet.  If a star appears only as a point of light, how can be tell how big the star really is?  We cannot just measure its size.  It turns out that we need two bits of information -- its distance, and its luminosity.  We earlier defined the Sun's luminosity as the total power output of the Sun (3.8 x 10²⁶ watts).  We will refer to the luminosity of other stars in units of the Sun's luminosity, so let's give it a symbol, L_sun.  A star with twice the power output of the Sun would have a luminosity of 2 L_sun.  Note that luminosity is an intrinsic property of a star, meaning that it does not depend on how far away the star is.  In fact, we often emphasize this by using the term intrinsic luminosity.

As it turns out, the nearest star other than the Sun, alpha Centauri, has slightly greater luminosity as the Sun.  But note that the Sun lights up our day on Earth, while Alpha Centauri appears only as a faint point of light, invisible except at night.  Obviously  the reason is that Alpha Centauri is very far away, while the Sun is nearby.  If we knew how the apparent brightness of an object changes with distance, could we compare the apparent brightness of the Sun and Alpha Centauri and tell how far it is to Alpha Centauri?
 

The sky centered on the star Kappa Orionis. Although Kappa Orionis looks much larger than the other stars in this image, that is an illusion caused by overexposure of the film.  Without the overexposure, the image of Kappa Orionis would be the same size as the faintest of the other stars in the image -- a single point of light. Is Kappa Orionis brightest because it is the star nearest to us in this image?  No, it is about 815 ly distant, while the star just above it is only 75 ly away!

 

It is easy to figure out how apparent brightness falls off with distance.  Consider the surface of a star, and all the energy passing through this surface each second.  This is the luminosity.  Now imagine another sphere centered on the star, but at some greater size.  The same energy per second must also pass through this larger sphere -- none of the energy disappears.  Now imaging a series of spheres, each one passing the same amount of energy per second.  The surface area of each sphere grows as the radius squared, and since the energy is the same through each sphere, it follows that the power per unit area (= brightness) falls as 1 over distance squared: 1/d².  That is, the brightness (energy flux) follows an inverse square law.

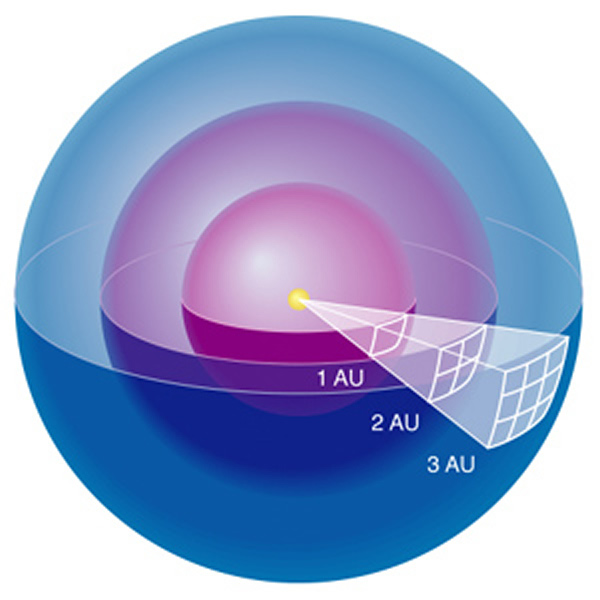
Figure 15.1 from the text.  The area of each sphere increases as the square of the distance, so the
flux per unit area falls as the square of the distance.  The apparent brightness is the same as the flux
per unit area, so the apparent brightness also falls as the square of the distance.

This gives the luminosity-distance formula:

apparent brightness = luminosity / (4p x distance²)

So of two stars with the same luminosity, the one that is farther away certainly has a smaller brightness.  But stars do not all have the same luminosity, as is shown by the case of Kappa Orionis, above.

Lecture Question #1

Measuring Distance
To sort out which stars are faint because they are far away, and which stars are faint because they have a low luminosity, we have to find some way to measure distances to stars.  This is a LOT harder than it may seem.  The whole problem of distances to objects in the universe is a fundamental one, and it has a name -- the distance scale.  The distance scale is a set of measurements going from small distances to larger and larger ones.  The first step in the astronomical distance scale is to know the distance to the Sun, 1 AU, which we now know to be 150 million km.  Once we know this distance, we can use the motion of the Earth around the Sun to look for small annual position variations due to parallax.  (Note that this is exactly the same cause as retrograde motion of distant planets).

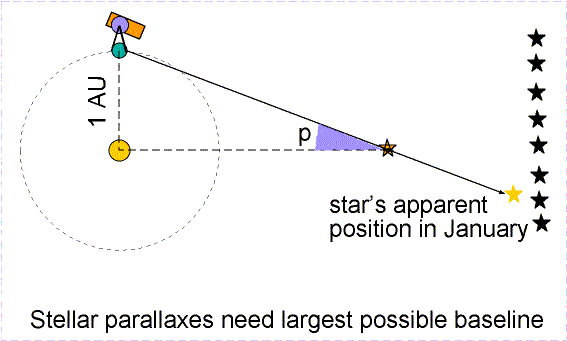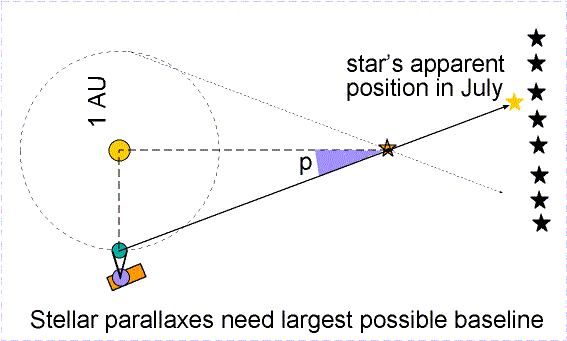
Measuring the position of nearby stars relative to distance stars over 6 months (January to July in the figure above), we can find that the star appears to shift a small angle p, called the parallax angle.  This turns out to be a very small angle, even for the nearest stars -- less than 1 arcsecond (1/3600 of a degree) for Alpha Centauri.  If a star were close enough to cause a shift of exactly 1 arcsecond, we would say that it is 1 parsec or 1 pc away.  The word parsec comes from the words parallax and arcsecond. Astronomers measure all distances in parsecs, not light-years.  But there is a simple relationship, 1 pc = 3.26 ly.  The reason astronomers use parsecs is that there is a particularly simple relationship between parallax and distance:

d (in parsecs) = 1 / p (in arcseconds)

We can measure angles to about 0.01 arcsecond, which means we can measure star distances using stellar parallax only to distances d = 1/0.01 = 100 parsecs (about 326 light-years).  Stars farther away than that show no measurable shift as the Earth orbits the Sun.  Stellar parallax gives the second step in the distance scale.  There are more steps that we will learn about later.

When we look at which stars in the sky show parallax, and so are the closest stars to us, we may be surprised to find out that many are very dim -- not even visible without a telescope.  Some brighter stars turn out to be pretty close, like Sirius (2.6 pc), Altair (5 pc), and Fomalhaut (7 pc), but many bright stars are so far away that they show no parallax.  That means the intrinsic luminosity of stars must vary enormously.

In the 1990's the Hipparchos satellite measured the parallax of almost 1 million stars at distances out to 200 pc (parallax of 0.005 arcsec). Before that, only a few thousand stars had accurately known parallaxes. Proposed space missions of the future are expected to be able to measure parallaxes out to 25000 pc--almost the entire distance across the galaxy!

Hipparchus and the Magnitude System

Astronomers measure the brightness of stars in magnitudes.  It is based on a system devised by the ancient Greek astronomer Hipparchus (c. 150 BC), who divided the brightness of stars into those of the first magnitude (the brightest), next brightest to 2nd magnitude, and so on down to those just visible with the naked eye as the 6th magnitude.  Modern astronomers have a problem, however, since they can see far fainter stars with the aid of telescopes and cameras.  They wanted to extend this system to fainter stars, so to do that they noted that it covered a range of about 100 in brightness (the brightest stars are 100 times brighter than the faintest).  To be quantitative, they set a range of 5 magnitudes as exactly equal to a factor of 100.  This has the effect of making some bright stars have even lower (brighter) magnitude than 1, so they go to zero, and even become negative.  We can assign a brightness to the Sun, and find that it is -26th magnitude!  So remember that the magnitude scale is kind of backwards -- the brighter stars have smaller magnitudes.

Note that these are apparent magnitudes.  If we get closer to Alpha Centauri, for example, it will appear brighter and the Sun, which we are moving farther away from, will appear fainter.  So apparent magnitude can change depending on where we are.  Astronomers like to express the brightness of stars also in absolute magnitude, so that it expresses the actual brightness of the star no matter how far away they are.  So we figure out how bright a star would appear if it were at a distance of 10 pc (32.6 ly), and call that the absolute magnitude.  The Sun would have a magnitude of about 4.8 (not very bright) if it were at a distance of 10 pc.  So its absolute magnitude is 4.8.

Lecture Question #2

If you look at a star catalog, you will see the star magnitudes, along with other information for the star.  Here is an example from the "Nearby Stars" catalog (stars within 25 pc):

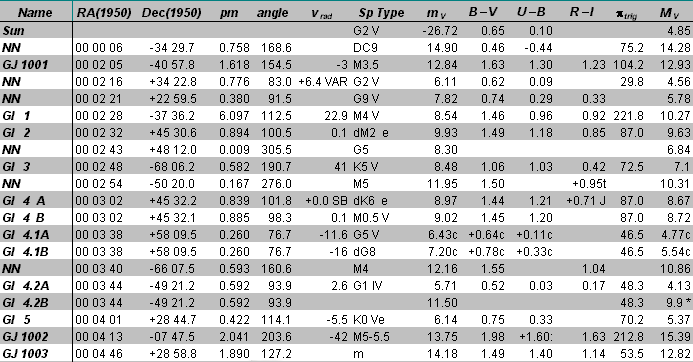
The columns marked m_V and M_V give the apparent and absolute magnitudes, respectively.   In order to know the absolute magnitude, note that we have to know the distance to the star.  For these nearby stars, we can actually measure their parallax.  For more distant stars we have to use another trick, which we will learn next time.

Remember our plot of the continuum spectrum of hot bodies, repeated below:

which shows how the spectrum depends on temperature.  Before we focused on the shift of the peak of the spectrum as the body gets hotter, which changes the color of the object -- cooler objects are red, and hotter objects are blue.  But notice how the overall level of the light also grows a lot with temperature.  Where the curves cross the visible spectrum, a 3000 K star is 3 or 4 orders of magnitude weaker than a 15,000 K star.  So you can see that a 15,000 K star is going to be 1000 to 10,000 times more luminous than a 3,000 K star, if they have the same size.  So for two stars at the same distance, a 15,000 K star is going to appear a lot brighter than a 3,000 K star.

As the foregoing statement implies, two stars may not be the same size.  In fact, there is a nice relationship between the luminosity of a star and its temperature, but it also depends on the size.  You can imagine that for two stars with the same temperature, but different sizes, the bigger star is going to be more luminous.  If we know the distance to a star (from stellar parallax), and its surface temperature (from the spectrum), then we can figure out its radius directly.  I am not going to show the equation for this, since this lecture has too many equations already, but you should keep in mind that knowing distance and temperature is all that we need to get the star's radius.

Stars have different colors, because of the differences in their surface temperatures.  We can also see spectral lines in the light from stars (see Lecture 6).  Here is the spectrum of a star with strong lines of hydrogen:
Spectrum of an A star, surface temperature 10,000 K, showing strong hydrogen lines.

Remember that these lines tell us what the star is made of, but the light between the spectral lines also tells us the temperature of the star.  To make sense of stars, we find it useful to try to classify them according to their spectrum.  Even before it was knows what the spectral lines were, scientists were able to take pictures of the spectrum and try to put them into some kind of order.  At Harvard College Observatory, Edward Pickering had a large collection of stellar spectra, and hired women from nearby colleges to help classify them.  To begin with, the spectra were classified according to how strongly the hydrogen lines stood out.  Williamina Fleming (1857-1911) was the first to do this, and called the types A, B, C, and so on according to the strength of the hydrogen lines.  The spectrum above is from an A star, because it has the strongest hydrogen lines.  Later, another woman, Annie Jump Cannon (1863-1941) recognized that by classifying not according to the hydrogen lines, but according to the star's color, or continuum spectrum, and thus in a temperature order, the spectra fell into a natural sequence.  She stuck with Fleming's letter designations, but reordered them so that, in temperature order they become O, B, A, F, G, K, and M.  Here, O stars are the hottest (bluest) and M stars are the coolest (reddest).

It is very important to memorize the order of these letters.  To help you, there are several mnemonics.  The classic one is "Oh Be A Fine Girl/Guy, Kiss Me." 

Here is what the new ordering of spectra looks like:

Adapted from data in the electronic version of "A Library of Stellar Spectra," by Jacoby G.H.,
Hunter D.A., Christian C.A.  Astrophys. J. Suppl. Ser., 56, 257 (1984).

Notice that the letter classification is subdivided with  a number, so the strongest hydrogen lines are in an A0 star, and an A1, A2, etc. are slightly cooler up to A9.  Then next cooler star is F0, and so on.  Notice also that the hydrogen lines are quite weak in the hottest stars (O stars).  The Sun is classified as a G2 star, so its hydrogen lines are not very strong.

Lecture Question #3

Strength of Hydrogen Lines and Temperature
We now know that all stars are basically made of the same stuff, and all have about the same amount of hydrogen (about 75%) and helium (about 25%), with trace amounts of other elements.  So why do the hydrogen lines stand out so strongly in some stars and not in others.  It turns out that the strength of the lines depends on the surface temperature of the star much more than the composition.   In the hottest stars, most of the hydrogen is ionized (the electrons are stripped off), so there are only weak lines (remember that the lines are due to transitions of electrons in orbit around the hydrogen nucleus).  In the coolest stars, most of the hydrogen is in the ground state, so the electrons are there, but they do not make the transitions needed to form the lines.  Only in stars with surface temperature around 10,000 K do we see hydrogen atoms in excited states, but not too ionized.

There is one more quantity that we will need before we can put all of this together and explain how we know so much about stars, even though they are mere points of light.  The missing quantity, the stellar mass, turns out to be the most important quantity of all.  Since all stars are made of the same stuff, there must be something that causes them to have different temperatures, and sizes, and of course this is just due to differences in stellar mass.  How can we measure masses?  For that we need a little help from the stars themselves -- basically we need the stars to come in pairs.  In that case, the stars will orbit around each other and if we measure their positions over a long enough time we can determine their orbital periods and their semi-major axes.  Then, using Kepler's Third Law (law of periods), along with Newton's modification of it:

P² = [4p²/G(M₁ + M₂)] a³

Once we measure the period P and the semi-major axis a, we can insert them into this equation and solve for the sum of the masses.  Let's try this for the visual binary star Xi Bootes, shown in the following figure:

It's period is 151.5 years, and its major axis is about 6 arcsec.  To find the semi-major axis, we divide this in half to get 3 arcsec, but we also need to know the distance to the star system to convert arcsec.  The distance to the star system (from their parallax) is 6.71 pc, for which the 3 arcsec semi-major axis becomes 3 x 10¹² m.  So plugging in 151.5 years for the period, and 3 trillion meters for the semi-major axis, we solve for the sum of masses to get 7 x 10²⁹ kg.  This turns out to be only about 1/3 the mass of the Sun, so both of these stars together have a mass less than 1/3 of the Sun.

Lecture Question #4

Other types of binary star systems
Another type of binary star is called an eclipsing binary. where one star actually passes in front of the other (causing an eclipse).  Algol (the star in Perseus, representing the evil eye of Medusa) is an eclipsing binary.   A final type is the spectroscopic binary, in which the stars are so close together that we cannot see them separately, but we know there are two because of the doppler shifts of their spectral lines.

We now have all the pieces to put together a remarkable classification of stars.  We know how to tell the temperature of stars, both from their colors and their spectral lines.  We know how to tell how far away the nearest stars are (from stellar parallax), and we know how to tell the masses of some stars (those in binary systems).  Next time we will put all of this together to create the most important graphic representation in astronomy, the H-R Diagram.