Jupiter's radius
is 71,398 km, or 11.2 times Earth's radius. That makes its volume
(11.2)3 = 1400 times that of Earth.
Its bulk density, however is only about 1330
kg/m3.
This is considerably less dense than Earth (5500 kg/m3)
and only slightly denser than water (1000 kg/m3).
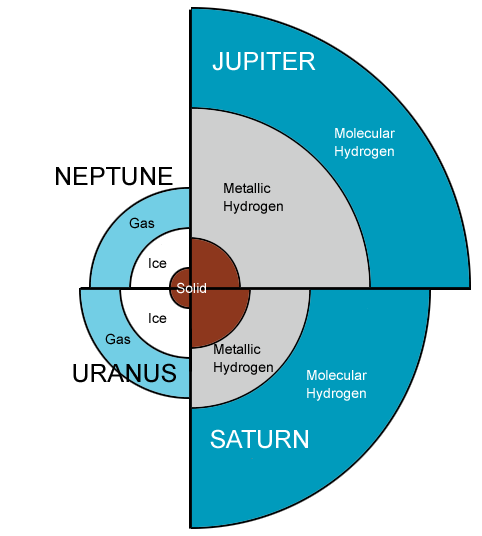
Jupiter is almost entirely made of gas, about 75% by mass of hydrogen and
24% helium, with only 1% of heavier elements. This is almost exactly
the composition of the Sun, giving an important clue to how Jupiter and
the solar system formed. Jupiter probably has a rocky core amounting
to several Earth masses.
The next layer out from the
core is liquid metallic hydrogen. This
exotic form of hydrogen can only exist at pressures exceeding 4 million
bars. Let's use our method of estimating pressure from Lecture 15 to get the core
pressure of Jupiter:
Pc = (2/3)
pG
<r>2
R2
= (1.4 x 10-10)
<r>2
R2
= (1.4 x 10-10)
(1330 kg/m3)2 (7.14x107
m)2
= 1.2 x 1012
Pa, or about 12 million atmospheres.
Liquid metallic hydrogen consists
of individual protons and electrons, where the electrons are able to flow
freely like those in a metal. At the temperature and pressure of
Jupiter's interior hydrogen is a liquid, not a gas. The temperature
in this layer is relatively high, between 11,000 and 40,000 K depending
on depth. This metallic layer is the source of Jupiter's strong magnetic
field -- 4x10-5
T at Jupiter's surface -- about the same as
that at Earth's surface, but remember that Jupiter's surface is much farther
out from the planet's center. Earth's magnetic field at the distance
of Jupiter's surface, RJ
= 71,400 km, is only
B = B0(r/RE)-3
= (4 x 10-5
T)(71400/6387)-3
= 2.86 x 10-8
T.
So Jupiter's magnetic field
is some 1400 times larger than Earth's. This mammoth magnetic field
traps huge numbers of energetic particles, so the particle radiation environment
at Jupiter is extreme. Spacecraft have to be carefully hardened
to withstand the radiation environment.
Above this metallic layer
is a layer of "ordinary" liquid hydrogen and helium, where the electrons
are bound to the protons. This ordinary liquid extends all the way
to near the surface, with a relatively thin layer of gas forming clouds
in Jupiter's atmosphere.
The albedo of Jupiter is
quite high, at 0.52, giving an equilibrium temperature of
Tss =
279 (1-A)1/4
(rp)-1/2
= 279 (0.84) (5.2)-1/2
= 103 K.
The observed temperature of
the cloud tops, however, is 130 K up to as much as 150 K. This leads
to the conclusion that Jupiter has an internal
heat source, probably left over from its gravitational contraction.
The "self-gravitational" potential energy of a body is
U = -GM2/R
,
which means that as a body contracts
(R decreases), the potential energy goes down (gets more negative).
According to the virial theorem, which
we have mentioned briefly before, 1/2 of this energy must be radiated away,
and the rest goes into heating the body. During Jupiter's formation,
it must have become extremely hot, and it is now slowly cooling down, but
it appears from what we know that Jupiter may still be generating heat,
perhaps continuing to contract slightly. How rapidly must it contract
to produce the excess heat that we see? Way back in lecture 8 we
discussed the flux of a black body, F = sT4
W m-2.
This flux of energy, when considered over the entire surface area of a
planet (4pR2),
gives a quantity called the luminosity,
L = 4pR2sT4
(watts).
We will be using this quantity
a lot next semester. It describes the total power (energy per unit
time) emitted by a spherical body. We expect Jupiter to have a surface
temperature of about T0 =
103 K, but it really has a temperature of
T
= 130 K, so the excess energy per second is
L = 4pR2s(T4
-T04)
= 4p(7.14 x 107
m)2(5.67 x 10-8)[(130)4
-
(103)4] = 6 x 1017
W.
We speculate that excess power
comes from a release of potential energy due to a slow contraction.
From the expression for potential energy above, the power released is
L = dU/dt = GM2/R2
dR/dt,
or
dR/dt = L R2
/ GM2, = (6 x 1017
W)(7.14x107 m)2
/ (6.67x10-11)(1.9x1027
kg)2
= 0.4
mm/year
Thus, it does not require much
contraction at all to release the observed amount of energy. Still,
over a billion years Jupiter would have to contract by 400 km, which seems
like a lot. It may be that the truth is some combination of contraction
and left-over heat.
Moving now out to the far reaches of the solar system, the separations of the planets get much larger. Jupiter is at 5.2 AU, but Saturn is almost twice as far, at 9.54 AU. This means it takes almost 30 years for Saturn to circle the Sun once. Uranus is again twice as far from the Sun as Saturn, at 19.2 AU, and takes 84 years to circle the Sun. It is so far from the Sun that it cannot be seen easily with the naked eye. Therefore, it was not discovered until 1781, by William (Wilhelm) Herschel. He originally named the planet George! (Georgium Sidus, for King George III of England). Likewise, Neptune was discovered only in 1846, at a distance of 1.5 times the distance to Uranus, 30.1 AU. It takes 165 years to circle the Sun once.
The discovery of Uranus was accidental, but the discovery of Neptune was a triumph of celestial mechanics. By studying the orbit of Uranus, an extremely tiny perturbation was discovered independently by J.C. Adams (1843) and U.J. Leverrier (1846). By using Newtonian celestial mechanics, they were able to predict the mass and orbit of the perturbing body. In 1846, Johann G. Galle found Neptune within 1o of its predicted location. However, Neptune's orbit diverged rapidly from the orbits predicted by the mathematicians, so if it had been searched for some years earlier or later, it would have been far from its predicted location. The text has a very interesting story about Galileo in this context. In 1613, some 234 years before Neptune's discovery, Galileo's drawings of Jupiter showed an object near Neptune's predicted position, and he even detected a small motion of the object with respect to a nearby star. However, he failed to follow up on the discovery.
All three of these gas giants have orbits of low eccentricity (Saturn and Uranus are nearly identical to Jupiter, with e = 0.056 and 0.048, respectively, while Neptune is even lower at 0.009), and low orbital inclination (2.49o, 0.77o and 1.77o, respectively). The inclination of their spin axes, however, are large: 26.7o, 98o, and 29o. The 98o for Uranus, in fact, means that it is nearly lying flat in the ecliptic plane, as shown in the image below. This means that the Sun shines on one pole for 1/2 of its year (that's 42 Earth years), and then on the other pole for 42 Earth years.
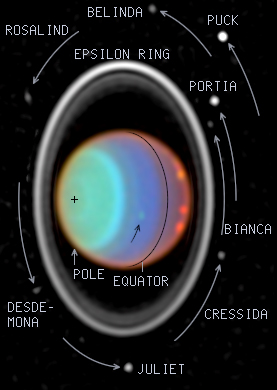
This is an infrared image of Uranus, its rings and moons,
taken by the Hubble Space Telescope.
All of these gas giant planets, including Jupiter, have ring systems, although only Saturn's rings are substantial enough to be seen from Earth. Jupiter's rings come directly from its moons, and are outside its Roche Limit. For Uranus and Saturn the rings are within the Roche Limit, and may be tidally disrupted bodies, although surprisingly small. The situation for Neptune is not so clear. We will discuss planetary ring systems in a later lecture.
Each of these outer gas giant planets has a magnetosphere. Saturn's is quite strong, again likely due to the metallic liquid hydrogen layer, as we saw with Jupiter. The surface magnetic field is 2.1 x 10-5 T, which is considerably weaker than Jupiter's, but certainly stronger than Earth's. At the distance of Saturn, the solar wind pressure can be quite variable, which greatly changes the size of the magnetosphere in a range from about 20 to 30 RS. Let's derive a general expression for the size of a magnetosphere, given the surface magnetic field of the planet and assuming that the solar wind pressure drops as 1/r2, where r is the distance from the Sun. Remember that a dipole field drops with distance from the center of a planet as
B = BS(r/Rp)-3 (1)
where BS is the surface magnetic field strength, and Rp is the radius of the planet. We know that the magnetosphere will extend out to a distance where the gas and magnetic pressures (proportional to B2) are equal, and that Earth's magnetosphere extends out to a distance of about 10 REarth. The magnetic field at this distance is B = BS(10Rp/Rp)-3 = 10-3BEarth. Since the gas pressure falls as 1/r2, the gas pressure at a distance rp (expressed in AU) from the Sun will be reduced by rp-2, so the magnetic pressure needed to match this is also lower by the same amount. The magnetic field strength needed is then reduced by the square root of this, or B = 10-3BEarthrp-1. This is the field strength needed at a distance rp (expressed in AU) in terms of the Earth's surface magnetic field. We need it in terms of the planet's surface magnetic field, which we get by equating this expression with equation (1), above, which expresses how the field falls off with distance from a planet. So we have
BS(r/Rp)-3 = 10-3BEarthrp-1
and solving for r, we get the final expression:
r = 10 (rp BS/BEarth)1/3Rp.
This remarkably simple expression gives the size of the magnetosphere for a planet of size Rp, a distance rp from the Sun, in terms of the planet's surface magnetic field strength, BS, and the Earth's surface magnetic field strength BEarth= 4 x 10-5 T. For Earth, of course, BS= BEarth, rp= 1, and Rp= REarth so we have r= 10REarth as required. At Jupiter, the surface field happens to be about the same as Earth's so we have BS= BEarth, rp= 5.2, and Rp= RJ so we have r= 17 RJ as was mentioned in the previous lecture. For Saturn, we have BS~ BEarth/2, rp= 9.4, and Rp= RS so we have r= 16.7 RS similar to the minimum distance mentioned above.
Uranus' magnetic field is odd in that it is not centered on the center of the planet and is tilted almost 60 degrees with respect to the axis of rotation. It is probably generated by motion at relatively shallow depths within Uranus. It's surface field strength is about the same as Saturn's, which predicts a magnetosphere of size, r= 21 RU.
Likewise, Neptune's magnetic axis is tilted about 46.8 degrees from the axis of rotation.