Go to EE495 Experiment | 1 | 2 | 3 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ECE Lab home
![]()
|
Go to EE495 Experiment | 1 | 2 | 3 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ECE Lab home |
|
Experiment 4: Frequency Modulation and Spectra of FM signals
Frequency Modulation: A Tutorial
A frequency modulated (FM) wave is most readily described by the carrier signal
|
|
(2.1) |
The instantaneous angle, (J( t ) , of the above cosine wave is the value in the brackets,
|
|
(2.2) |
The derivative of q ( t ) is the instantaneous radian frequency w ( t ) of the FM signal. Dividing that by 2p produces the instantaneous frequency f ( t ), given by
|
|
(2.3) |
It is now clear that the instantaneous frequency of the FM signal varies around the carrier frequency fc by an amount k f x ( t ), where kf is the modulation constant. Positive values of x ( t ) produce increases in f ( t ), whereas negative values of x ( t ) produce decreases in f ( t ). If x ( t ) is restricted by
|
| x ( t ) | £ xmax |
(2.4) |
then the frequency of the FM wave varies around fc by ± kf xmax This is the reason that kf xmax is referred to as the maximum frequency deviation of the FM wave
|
( Df )max = kf xmax |
(2.5) |
It is nearly impossible to find the spectrum of an FM wave except for special waveforms of x ( t ). The simplest is the sinusoidal case, given by
|
x ( t ) = Am cos wmt |
(2.6) |
and we observe that for this sinusoid xmax = Am, hence the maximum frequency deviation in this case is
( Df )max = kf Am (2.7)
For this modulating waveform, (2.1) becomes
 (2.8)
(2.8)
The notation can be simplified by defining
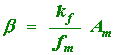 (2.9)
(2.9)
so that
xc( t ) = Ac cos ( wct + b sin wmt ) (2.10)
It is obvious from the last equation that the parameter b is the peak phase deviation of the signal. It is also referred to as the modulation index. It is noteworthy that the modulation index is inversely related to the modulation frequency fc.
We are now in a position to find the spectrum of the signal in (2.10). The easiest way to proceed is to write (2.10) in the exponential form
![]() (2.11)
(2.11)
which can be recast into
![]() (2.12)
(2.12)
In the above we use a well known mathematical identity in terms of In(I''), the Bessel functions of the first kind,
 (2.13)
(2.13)
to obtain
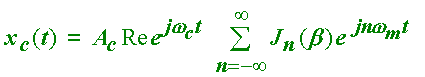 (2.14)
(2.14)
or
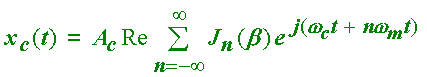 (2.15)
(2.15)
| Table 2.1: A short table of Bessel Functions. | |||||||
| n | Jn(0.1) | Jn(0.2) | Jn(0.5) | Jn(1.0) | Jn(2.0) | Jn(5.0) | Jn(10) |
| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
1.00 0.05 |
0.99 0.10 |
0.94 0.24 0.03 |
0.77 0.44 0.11 0.02 |
0.22 0.58 0.35 0.13 0.03 |
-0.18 -0.33 0.05 0.36 0.39 0.26 0.13 0.05 0.02 |
-0.25 0.04 0.25 0.06 -0.22 -0.23 -0.01 0.22 0.32 0.29 0.21 0.12 0.06 0.03 0.01 |
The above is identical to
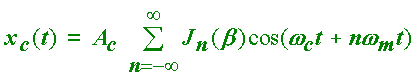 (2.16)
(2.16)
We finally
have the result that allows us to plot the spectrum of the FM wave for a sinusoidal
modulating signal. Some values of Jn(b)
can be found in table 2.1 as well as in figure 2.1.
Very thorough listings can be found in E. Jahnke, F. Emde and F. Lösch,
Tables of Higher Functions, McGraw-Hill Book Company, 1960. A very affordable
(but older) paperback version, by the first two authors, is available from Dover
Books.
The procedure that was used to find the spectrum of
the single tone modulated FM wave described in (2.10) can be used to find the
spectrum of the multitone modulated signal
xc( t ) = Ac cos ( wct + b1 sin w1t + b2 sin w2t) (2.17)
to obtain the result
 (2.18)
(2.18)
The above procedure can be extended to more than two tones, but it can become rather messy. The above equation tells us that this wave contains four different kinds of frequency components.
 |
| Figure 2.1: Curves of Bessel functions. |
1. There is the carrier of magnitude
Ac J0 ( b1)J0
( b2)
2. There are sidebands lines at fc
±
nf1
due to the first tone.
3. There are sidebands lines at fc
±
mf2
due to the second tone.
4. There are sidebands lines at fc
±
nf1
±
mf2 due
to both tones. This is somewhat surprising when compared to linear
modulation schemes, such as AM, DSB-SC and SSB, where such lines would not appear
at all. But FM is a non-linear
modulation scheme, so this is not surprising after all.
In your report address the item below.
1. Derive the result in (2.18) by starting with (2.17) and using (2.13),
Frequency Modulation - Part 1
The Wavetek generator can be used as an FM modulator by applying a modulating signal to the external input. This signal will change the frequency of the oscillator from the nominal value shown on the dial. To use this feature intelligently we have to know the change in frequency produced by a given external voltage.
Obtain data for a plot of output frequency as a function of input voltage. for
DC input voltages in the range of approximately 1 volt. Set the frequency with
|
Table 2.2: Values of b for zeros of Bessel functions |
|||
| J0 ( b ) = 0 | J1 ( b ) = 0 | J2 ( b ) = 0 | |
| b
for 1st zero b for 2nd zero b for 3rd zero b for 4th zero b for 5th zero |
2.40 5.52 8.65 11.79 14.93 |
3.83 7.02 10.17 13.32 16.47 |
5.14 8.42 11.62 14.80 17.96 |
zero input voltage to approximately 1 Mhz. Use a frequency counter for accurate determination of frequency. Use a power supply for the DC input voltage. (A 10 ÷ 1 voltage divider across the power supply will make it easier to adjust the voltage. ) Draw a best fit straight line through your data. Since the slope of this straight line is the modulation constant kf kHz/volt, you can now determine kf when the Wavetek is used as an FM modulator .
Frequency Modulation - Part 2
The measurement of frequency
deviation for a time varying modulating signal is not an easy thing to do in
general. However, if the modulating signal is sinusoidal and we have a spectrum
analyzer available, there is a nice method available for making accurate deviation
measurements. This is based on the fact that at certain values of the modulation
index some of the spectral components go to zero. We will use this method to
measure the deviation of an FM signal produced by the Wavetek generator for
a sinusoidal modulating signal and will compare our results with those of part
1. This will determine if the sensitivity of this modulator is the same for
AC signals as it is for DC signals.
Apply a sinusoidal signal of some convenient frequency
( 10 kHz) to the modulation input (you can use the counter to measure the frequency
accurately) and slowly increase the amplitude of the signal, starting with zero,
until the carrier component goes to zero, or reaches a minimum. Measure the
amplitude of the 10 kHz signal at this point.
Table 2.2 contains zeros of the Bessel functions. Using
this table calculate the frequency deviation. Repeat this procedure using nulls
of the first side band and other nulls of the carrier until you reach a deviation
in the neighborhood of 100 kHz. Using this data you can plot peak deviation
as a function of the peak value of the modulating signal on the same sheet as
the plot of part 1. How do the two curves compare ?
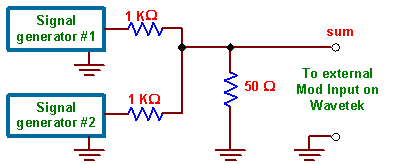 |
| Figure 2.2: Method for summing two signals. |
Frequency Modulation - Part 3
Using the values for the sidebands given in table 2.1, adjust the amplitude of the modulating signal to produce modulation indices of 0.2, 1.0 and 5.0. Sketch the spectra for these values. Approximately how many sidebands are needed to represent the signals in each case ?
Frequency Modulation -Part 4
Using the same amplitude square waves as the sine wave amplitudes in part 3, sketch the spectrum for a square wave modulating signal. This will give you an idea of what the spectrum looks like when transmitting data using the FSK (frequency shift keying) method.
Frequency Modulation -Part 5
In this part we will examine the spectrum of an FM signal where the modulating signal is the sum of two sinusoidal signals. This will illustrate the non-linear nature of FM. The mathematical expression for such a signal is given in (1.15) and (1.16). gives insight into the spectrum that can be expected. The sum of two signals can be obtained as shown in figure 2.2.
Choose the two audio frequencies so that the sum f1 + f2 and the difference f1 - f2 will not fall on harmonics of f1 or f2. For example choosing f1 = 20 kHz and f2 = 10 kHz would not be a good choice as f1 - f2 would fall on top of f2.
With generator #2 disconnected adjust amplitude of generator
#1 to make b1
= 1. Now do the same backwards to adjust for b2
= 1. Now connect both generators.
Note the appearance of spectral lines at
fc
±
( f1
- f2
) and fc
±
( f1
+ f2
) that were not present when either generator #1 or generator
#2 was connected alone. Record the amplitudes and frequencies of terms large
enough to be measurable. Identify them as the carrier, lines at
fc
±
nf1
due to the first tone, lines at fc
±
mf2
due to the second tone and lines at
fc
±
nf1
±
mf2
due to both tones.
Compute
the theoretical amplitude of these terms using (1.16), and compare measured
and calculated values by tabulating the results neatly. Discuss how these results
indicate that FM is a non-linear type of modulation.
|
Go to EE495 Experiment | 1 | 2 | 3 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ECE Lab home |
|