Fig. 1:
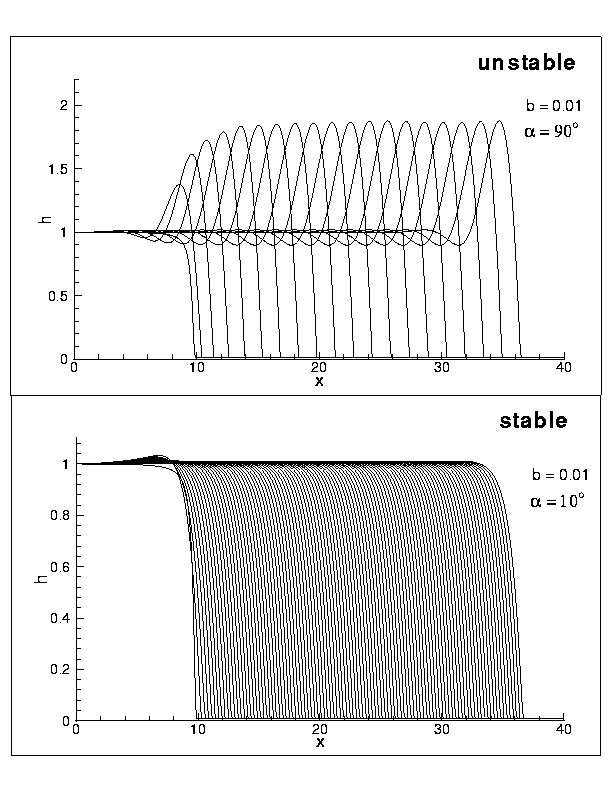
The competition between the downhill component of gravity and the surface tension leads to formation of the capillary ridge close behind the contact line (viz. Fig. 1). The presence of this ridge (also observed in the experiments) implies instability of the contact line with respect to the perturbations in the transverse direction. For small inclination angles, however, the destabilizing effect is weaker, and the capillary ridge is smaller. For these angles, there is a discrepancy between the experimental and theoretical results - the theory predicts stability, while the experiments show an unstable contact lines. The source of this discrepancy is not yet clear.
Recently it was proposed that this question could be understood based on the hypothesis of transient amplification of the microscopic noise, always present on a solid surface. In the framework of the precursor film model, this noise can be modeled via perturbations of the precursor film thickness. As the bulk of the fluid film flows over these perturbations, they can be amplified and lead to macroscopic effects.
Figure 2 shows snapshots of the film profile as it flows down an incline, in +x direction. Part a) shows strongly unstable situation (vertical plane), characterized by well developed capillary ridge. Part b) shows flow which would be stable without the presence of the perturbation. The upper inserts in a) and b) give the maximum film height as a function of time, for a perturbed flow (solid line) and unperturbed one (broken line). The perturbation itself is shown in lower inserts (note the different scale here; the perturbation is almost invisible on the scale defined by the film thickness). The unperturbed precursor film thickness is b=0.01, scaled by the film thickness far upstream.
Fig. 2:
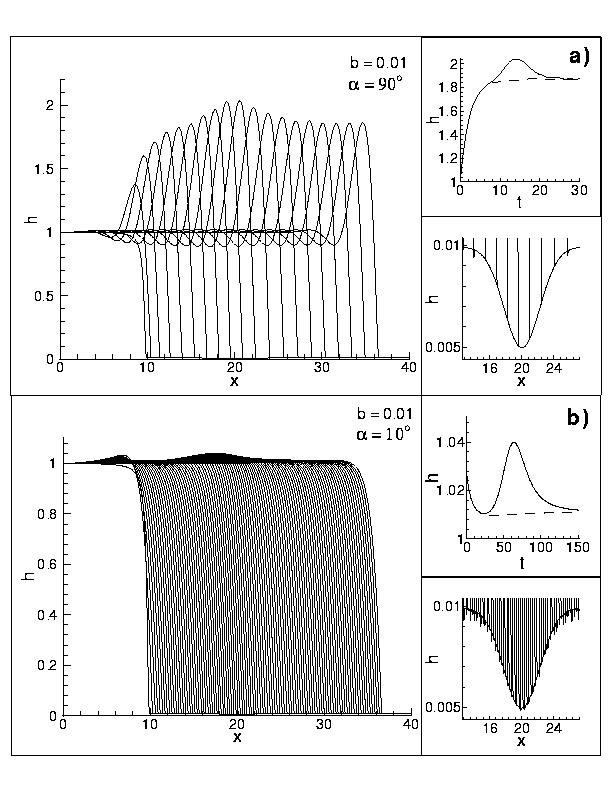
We observe that, indeed, a considerable amplification of a small perturbation of the precursor film can be achieved. As expected, the effect is much stronger for large inclination angles (viz. Fig. 1, where a well developed capillary ridge is present for the unperturbed flow as well). Still, a finite size ``bump'' is produced even in the case of a stable film, meaning that the instability can be induced by a small perturbation of the precursor film thickness (Fig. 2b). Even more interestingly we find that there is a characteristic width-scale for such perturbations to have significant effect. Only perturbations wider than a certain cut-off width (comparable to the capillary length), can induce instability. Since the required width-scale is larger than the typical scale introduced by ordinary surface roughness, it is not expected that the surface roughness can be the sole cause of the experimentally observed instabilities. Full 2D simulations (see here) are required to give more accurate answers to these questions.