Home MATH 112 Simulation Gallery

Simulation Gallery

Elemetry Spin Immersed in a Magnetic Field

Landau-Lifshitz Equation:
time evolution of ferromagnetic materials

Consider an elementary ferromagnet which has an average magnetic moment, for example, a small sphere of iron, fixed in space. When immersed in an external magnetic field (H), the sample's magnetic moment (M) will dynamically reorient according to the Landau-Lifshitz equations. One observes both a circular precession about the magnetic field axis, and energy losses which dampen the motion until the spin comes into alignment with the magnetic field. In a real material, this realignment process occurs on the order of nanoseconds.

Principles of Computational Physics

Electromagnetic Waves, Optics, Software Engineering

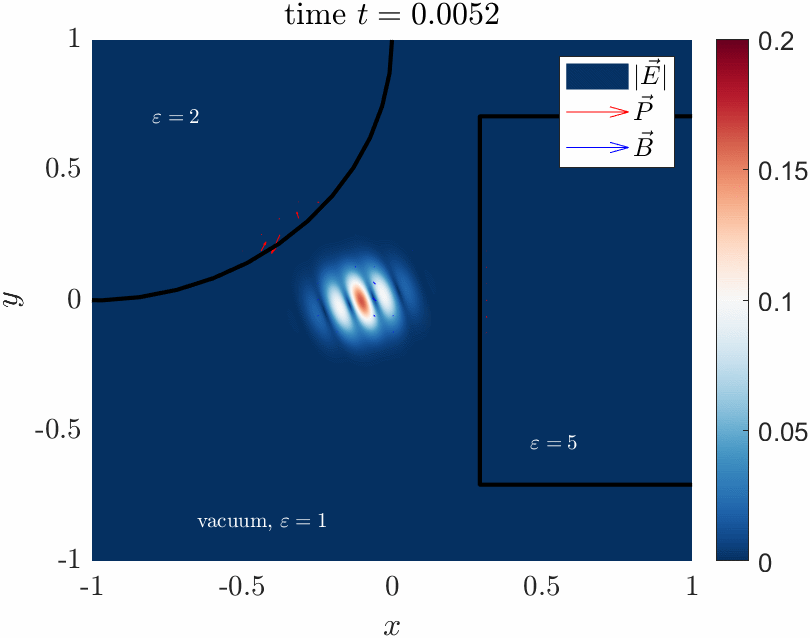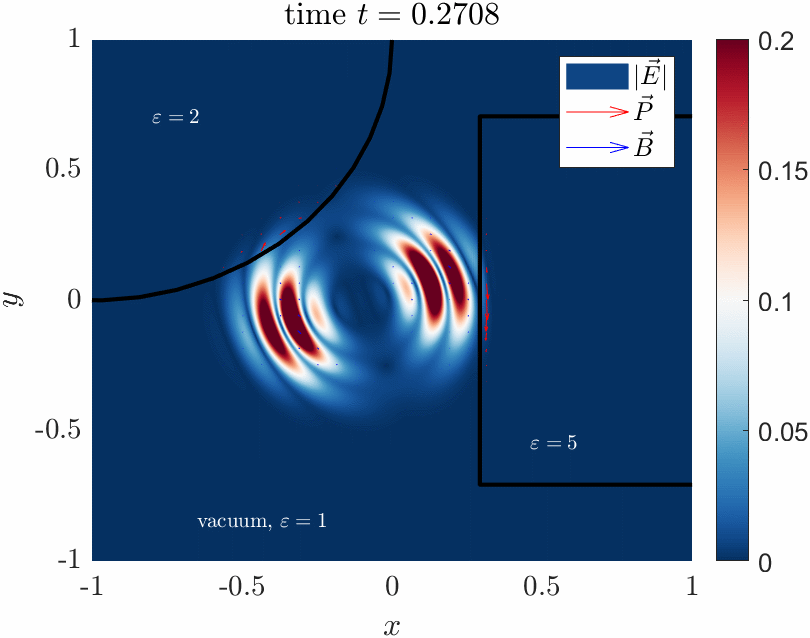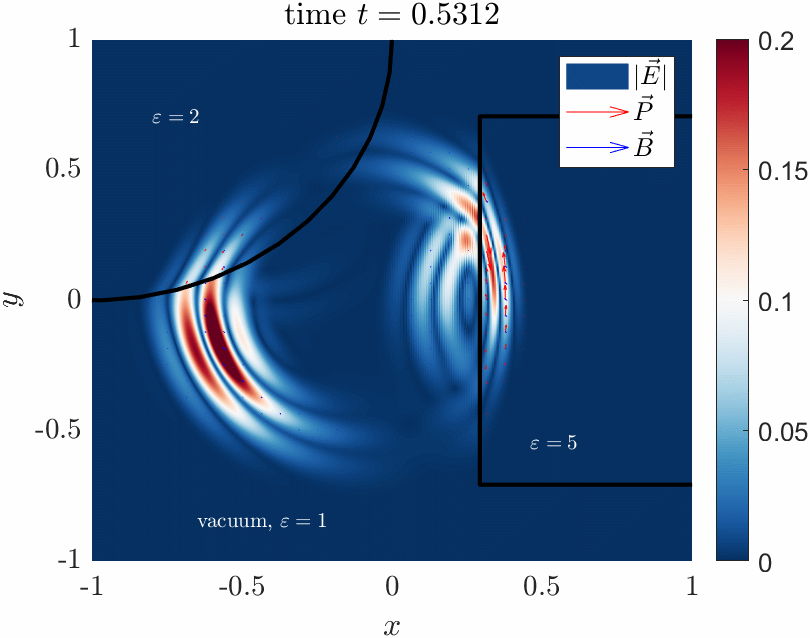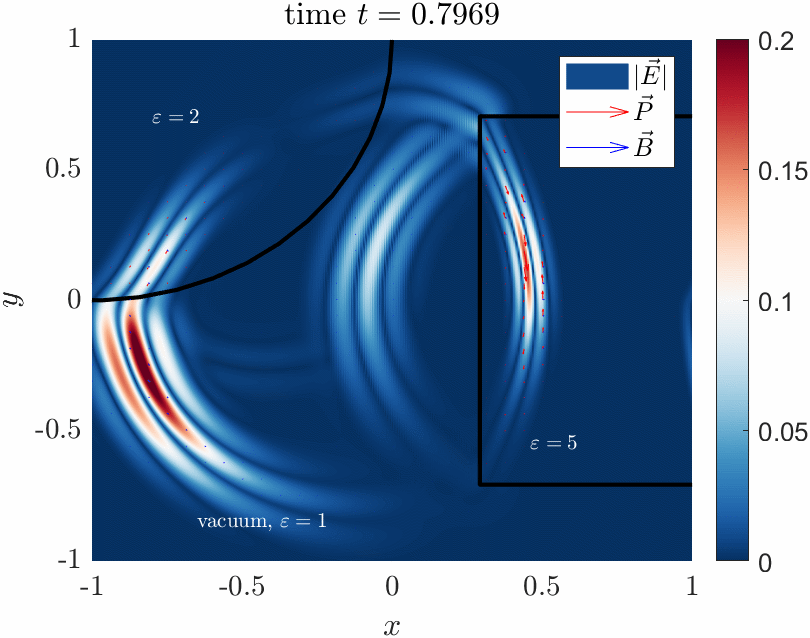
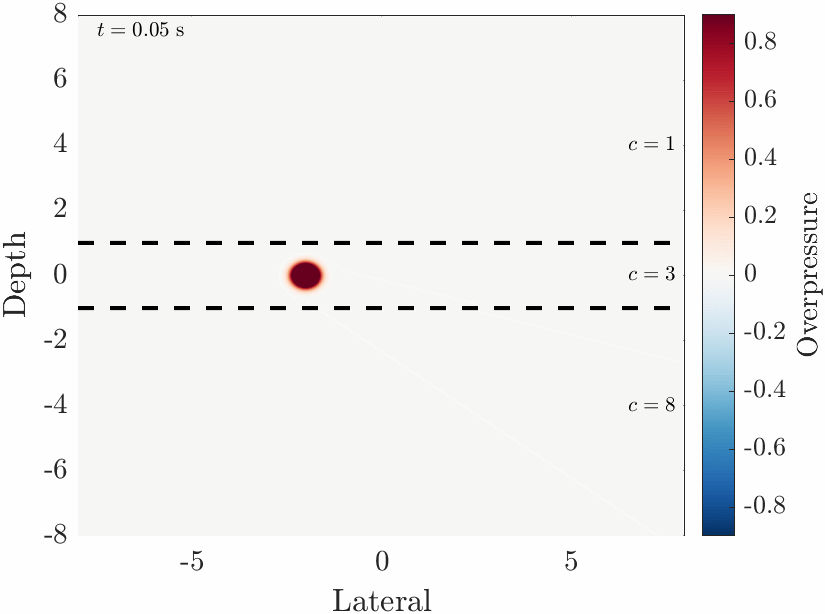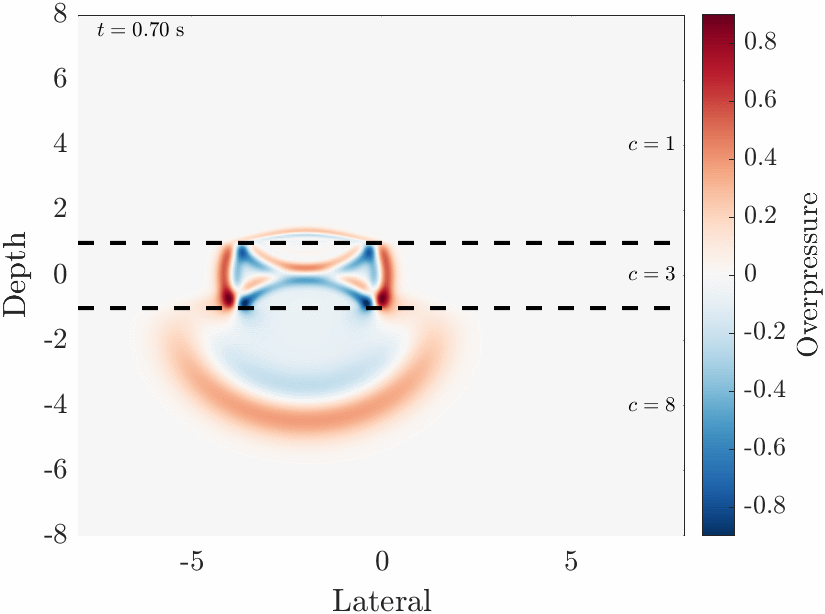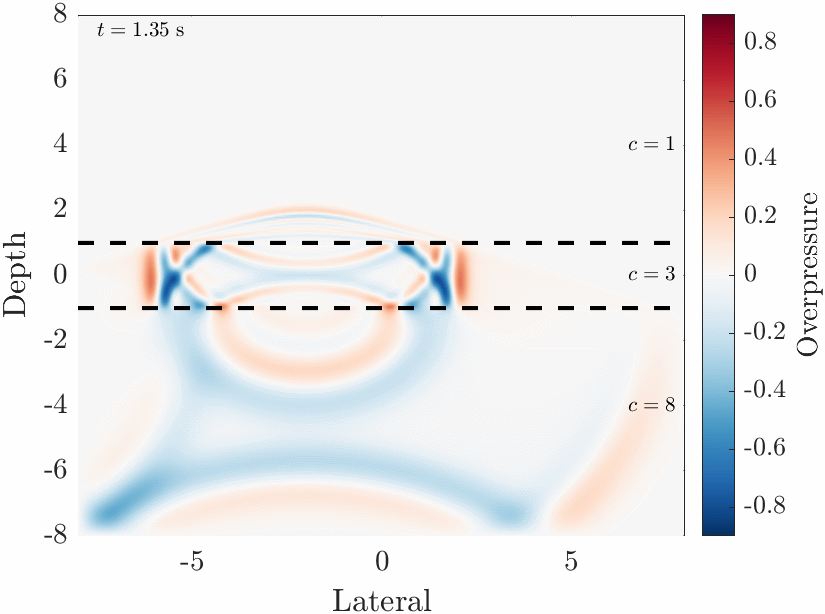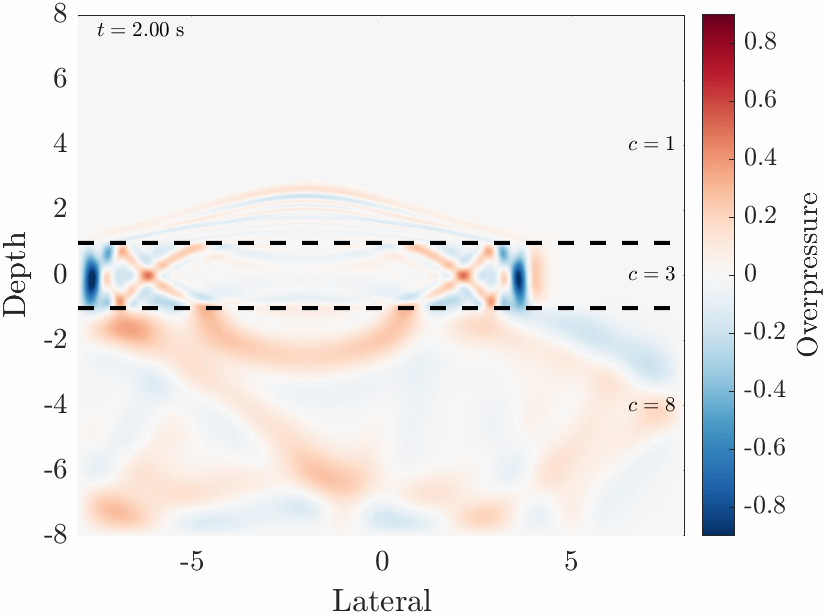
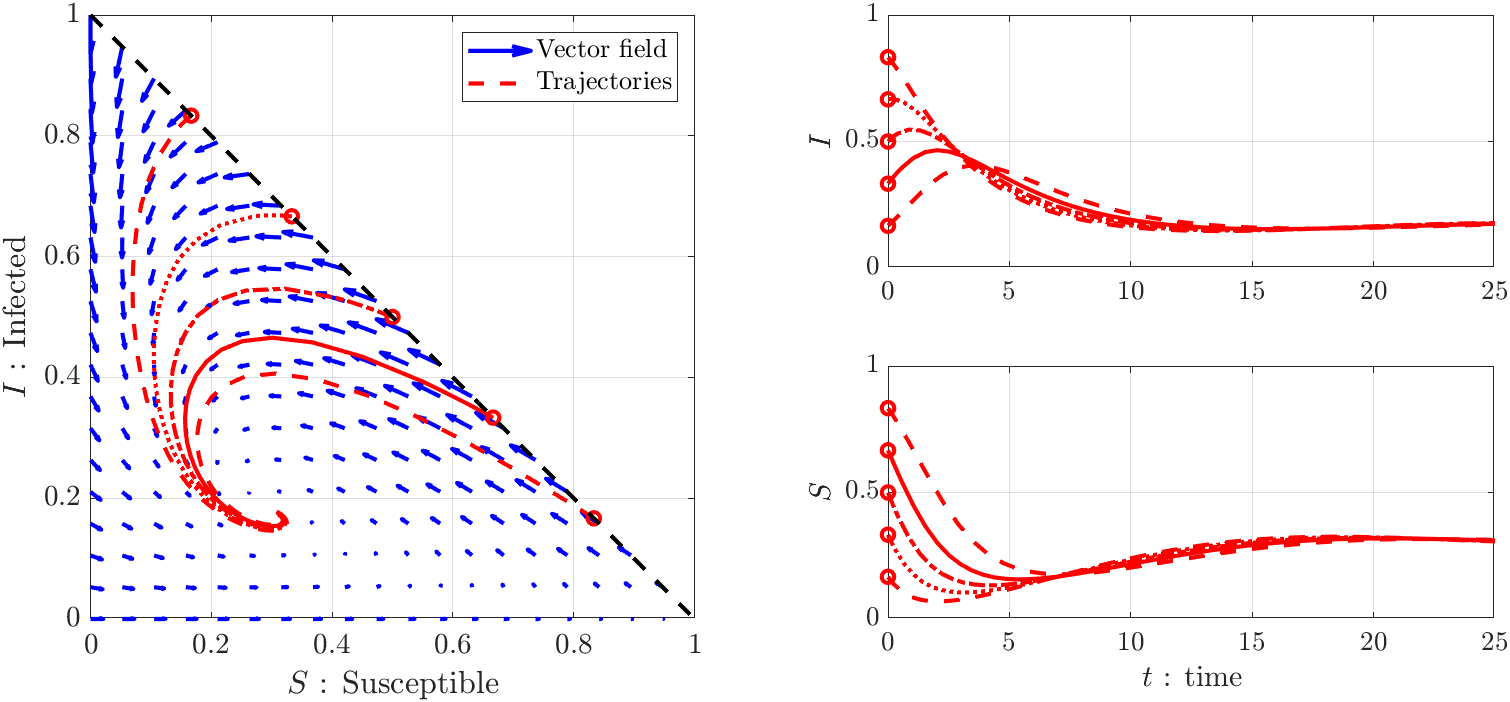
Pictured is a numerical simulation of maxwells equations in a mixed vacuum / solid dielectric system which I developed in MATLAB. This demonstrates some basic optics, like reflection and refraction of the wave into the slower dielectric material.

Since optics problems like this are so diverse, and subject to innumerable instances, one would have to spend hours on modifications of the base methods, just to solve a very similar optics problem. The solution is one of software engineering rather than physics, you need a code base that takes advantage of commonalities among all conceivable applications. Here I backend all the vector calculus into simple macros and do the same with the solid geometry, so that a user doesn't need to think about it. I can then develop a simulation environment as a class in and of itself, with its time evolution, and plotting routines stored as internal methods. Call it a “C++ inspired” implementation. This object-oriented approach makes the codebase lightweight, customizable, and user friendly. It anticipates the needs of a beginning user, as it is you need only a few lines of code to produce basic scripts and solutions. Furthermore, it’s such that a more advanced user can add functionality to it without breaking the old methods.

Try it out on my GitHub.

Nonlinear Waves

Nonlinear Schroedinger Equation

The nonlinear schroedinger equation is related to shallow water waves, and is thought to be important for the study of rogue waves Despite its name, it does not serve any model for quantum physics.

Sonar and Oceanography

Emergent Structure in Stratified Fluids

Media of stratified density propagate soundwaves at different speeds. This leads to refraction and reflection of waves according to Snell's law. The consequences have big implications for the use of sonar in the ocean, and seismic imaging, among other things. A stratified strip can lead to a channel which conducts waves due to its internal reflections. This can facilitate long distance communication, as the wavefront is confined, and does not dissipate energy into the whole space. The internal reflections also cause an aggregation of echos of the signal to propagate along the corridor. The nature of signal distorsion at an interface between two regions of different sound speeds, c, leads to diverse categories of emergent structures called ''interfacial waves''. One example is the Rayleigh wave: from a sound source in a faster media, its refraction into a slower media creates a planar wave front propagating into the slower media

Epidemic Modeling

Dynamics of Infectious Deseases with the SIR model

The SIR (Susceptible, Infected, Recovered) models are a class of differential equations for modeling the spread of infectious diseases. In the model, the population is divided into groups which may transition to other groups. Susceptible becomes infected at a certain rate, infected becomes recovered (and immune) at a certain rate, and this relation is written (S->I->R). Variations and modifications of this simple model help inform the spread of various recurrent epidemic illnesses such as measles and influenza, and now much more recently, Covid 19. Dimensional analysis on infection rates can establish how virulant the diseases is, and whether `Epidemic' will (may) occur. Presented above is the phase diagram and some example trajectories of the S->I->R->S model, where the recovered population loses its immunity to the illness at a certain rate. Here one observes, absent any external input, that the infected population settles down to a constant nonzero value, and the illness is not eradicated.

Sports Ranking and Forecasting

The Colley Matrix Method

How can one objectively measure performance? This is Wesley Colley's method for ranking sports teams against one another. I once tried to use this in a limited way to predict the outcome of the 2014 world cup using data from friendlies and preliminary matches. My prediction had Argentina winning the tournament, though we would later find them eliminated in the final. I programmed it more extensively to rank teams from March Madness 2017 in the example pictured to the left.

The method is bias free, prefiguring the average rating to be 1/2. It is designed to only use very limited information about the teams, just their wins and losses. The method derives a matrix of interactions between the teams in order to rank all of them simultaneously by solving a linear system. Therefore, teams which never played eachother can still be ranked against one another by way of comparison to their common opponents. This enables the analysis of tournaments with a limited number of games.

For more details on the Colley method see Here to Download Colley's Original Paper.

Download my MATLAB code and data


click to enlarge

Traveling Wave

Viscous Burgers Equation

The Viscous Burgers Equation is one of the simplest nonlinear advection diffusion equations. Analytical solutions exist via the Cole-Hopf transformation. Interestingly, it is known to admit a simple traveling wave solution under certain conditions. Pictured right, numerical solution of the traveling wave via explicit forward-Euler method.
Download my MATLAB code

Shock Wave and Solution Breakdown in Finite Time

Inviscid Burgers Equation

The Inviscid Burgers Equation enables the formation of "Shockwaves" due to its lack of any diffusion terms. For certain initial conditions the waveform will develop a steep gradient which appears to want to tumble over itself. After formation of the shock, numerical solutions breakdown entirely, and analytic solutions (if they are avaliable) are considered invalid after the time of shock formation.
Pictured right, shockwave formation and solution breakdown, numerical solutions using 3 different orders of Adams-Bashfourth methods

Mandelbrot Set

Zooming in on Mandelbrot set

Scientia potentia est