One approach is to modify the governing PDE through the introduction of a source or penalty term over the obstacle region. The penalized PDE is then attractive to solve since there is no need to directly impose boundary conditions. Unfortunately, due to the presence of an analytic boundary layer, penalty methods converge very slowly to the underlying PDE (for Navier-Stokes the rate is O( η 0.5) in the penalty parameter η ). The resulting slow convergence in η limits the practicality of conventional Fourier penalty methods to 1st order for Navier-Stokes (and also 1/2 order for Maxwell's equations)
My research is focused on developing active penalty methods which improve the analytic convergence rate (high order in η) of the penalized PDE to the underlying PDE. The subsequent gain in η - convergence rate translates directly into a high order Fourier method. I also focus on practical details, such as the efficient construction of the penalty function in two or three dimensions, as well as the stability and conditioning of the active penalty term. In work with J-C. Nave, we demonstrate 2nd and 3rd order convergence for the heat and Poisson equation (in one and two dimensions), and 2nd order convergence for Navier-Stokes.
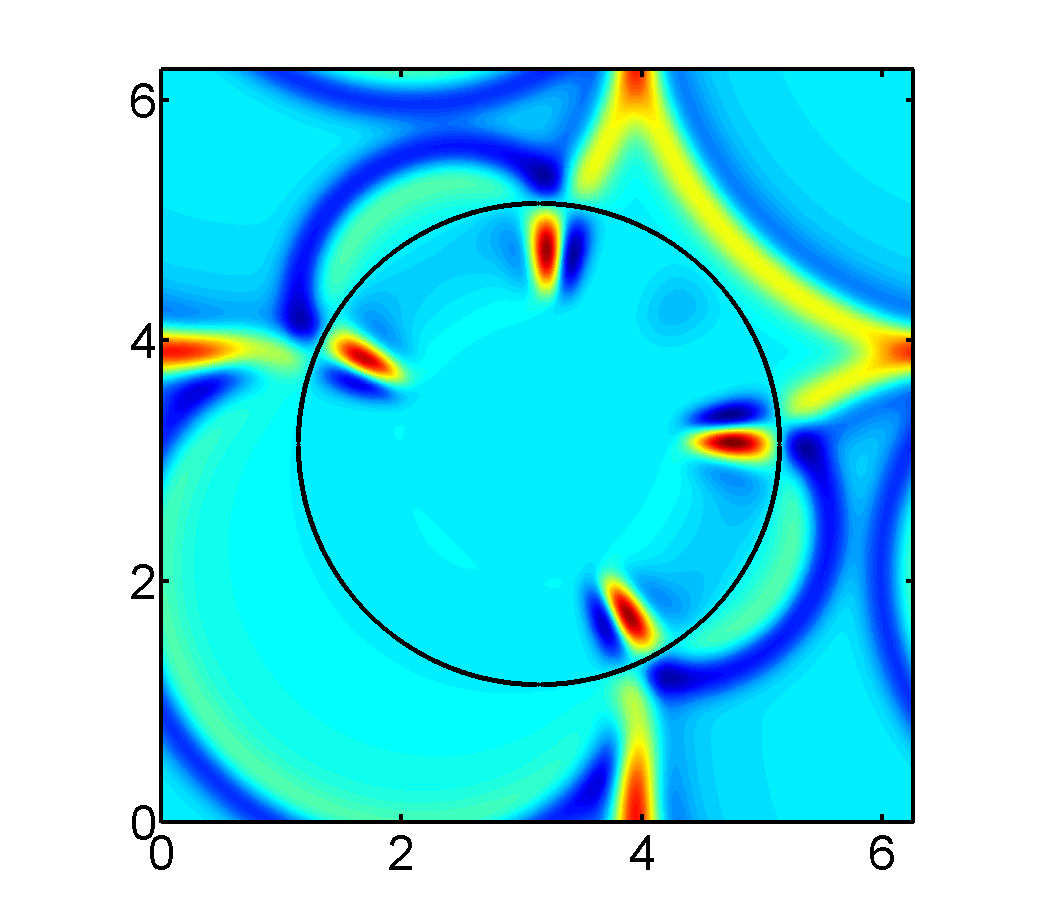
Above: A full time-dependent scattering calculation of a perfect electric conductor (PEC) for a transverse mode (TM) of Maxwell's equations. The calculation was done using Fourier spectral methods and an active penalty term which controls the solution inside the obstacle region while enforcing the boundary condition to high order. In the above calculation, we obtain a convergence rate (in the maximum norm) of order 2.5 while a conventional penalty method yields a convergence rate of 0.5.
Pressure Poisson Equations (A Projectionless method)
Even in simple domains, the numerical solution of the incompressible Navier-Stokes equations is difficult since the velocity components are coupled (by the pressure) through the divergence constraint and velocity boundary conditions. Numerical methods which decouple the velocity and pressure, such as fractional-step or projection methods, often suffer from numerical boundary layers or low order in time. For instance, the review paper by Guermond, Minev and Shen, (Comput. Methods Appl. Mech. Engrg. 195 (2006) 6011-6045) provides a nice background on the difficulties associated with projection and fractional-step methods.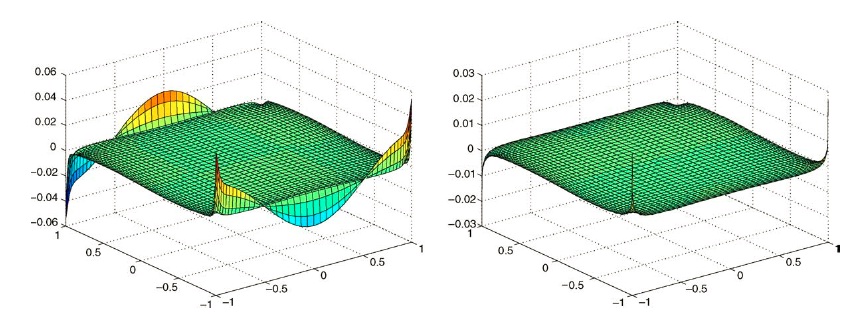
Above: Image is from Guermond et al. and illustrates the O(1) numerical boundary layer errors in the pressure for (left) projection method, (right) fractional-splitting with consistent boundary conditions. In work with R. Rosales [arxiv:1011.3589], we derive a set of consistent pressure boundary conditions and recast the Navier-Stokes equations as a pressure-Poisson system. This allows us to efficiently solve the Navier-Stokes equations (as efficiently as a projection method) without numerical boundary layers.
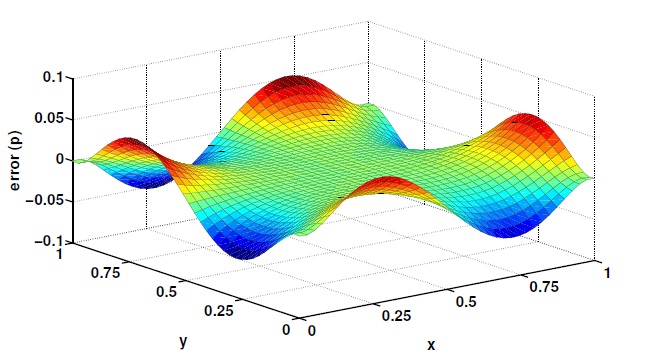
Above: Shows the error in the pressure produced by our scheme for the same test as in the paper by Guermond et al. Note the error in the pressure field converges uniformly with no numerical boundary layers. The total amplitude of the error may be reduced by decreasing the grid spacing.
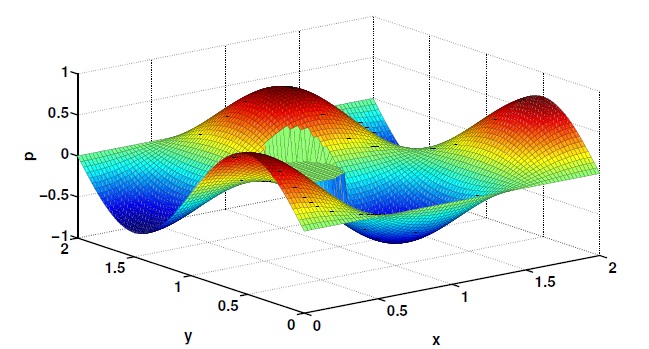
In addition, we perform similar tests in more complicated domains, such as flow around a circle. Here the domain is immersed in a regular grid. The above figure shows the pressure, and does not have a numerical boundary layer. Another advantage with the approach, is that the resulting equations may be discretized (in theory) to any order in space and time, provided that the discretization scheme is stable and consistent.
Energy Driven Pattern Formation in Material Science
A wide class of materials (crystalline solids, diblock copolymers) are modelled through the introduction and minimization of a non-convex and often non-local energy functional. Here the derivative terms in the functional typically pick out a preferred length scale, while the nonlinear terms generate a preference for certain constant values. The result is that for different material parameter values, the energy functionals drive the solution into a given pattern or structure.


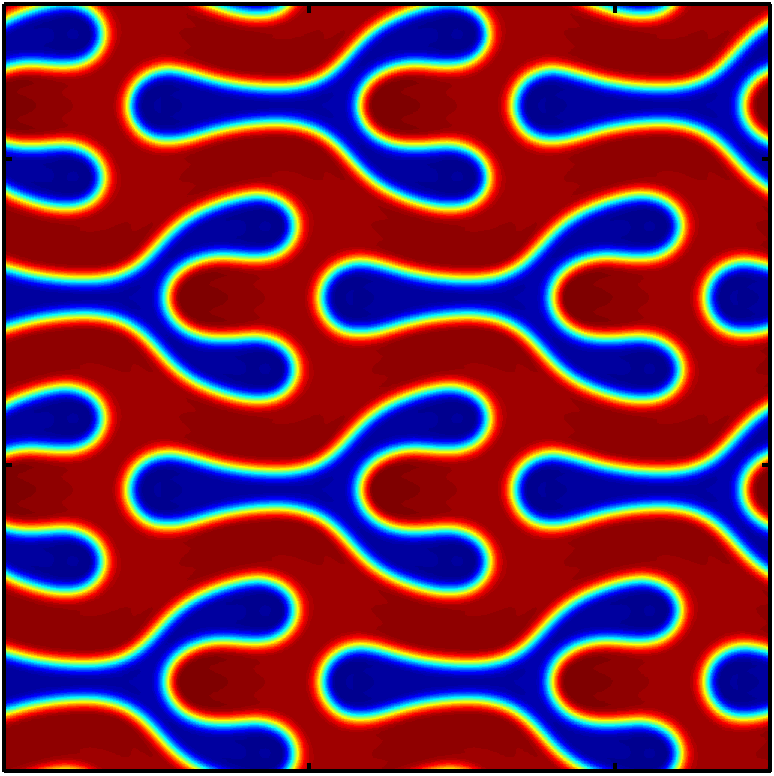


Above: A collection of local minimizers to the Ohta-Kowasaki functional. Due to the non-convexity, the functional can have many minimizers for one parameter value. The hex lattice (top left) has the lowest energy. These states were obtained using an H-1 gradient flow along with a spectral projection algorithm and different random initial data.
In work with R. Choksi and J-C. Nave, we devise a strategy for verifying whether the constant state is the global minimizer for a wide class of non-convex energy functionals. This requires a global approach to the energy landscape by examining distant states. We do so by deriving a nearly optimal global lower bound functional. Computation of the lower bound functional also provides an efficient, accurate estimate (for instance much better than linear instability analysis) of the order-disorder (liquid-solid) phase transition curve.
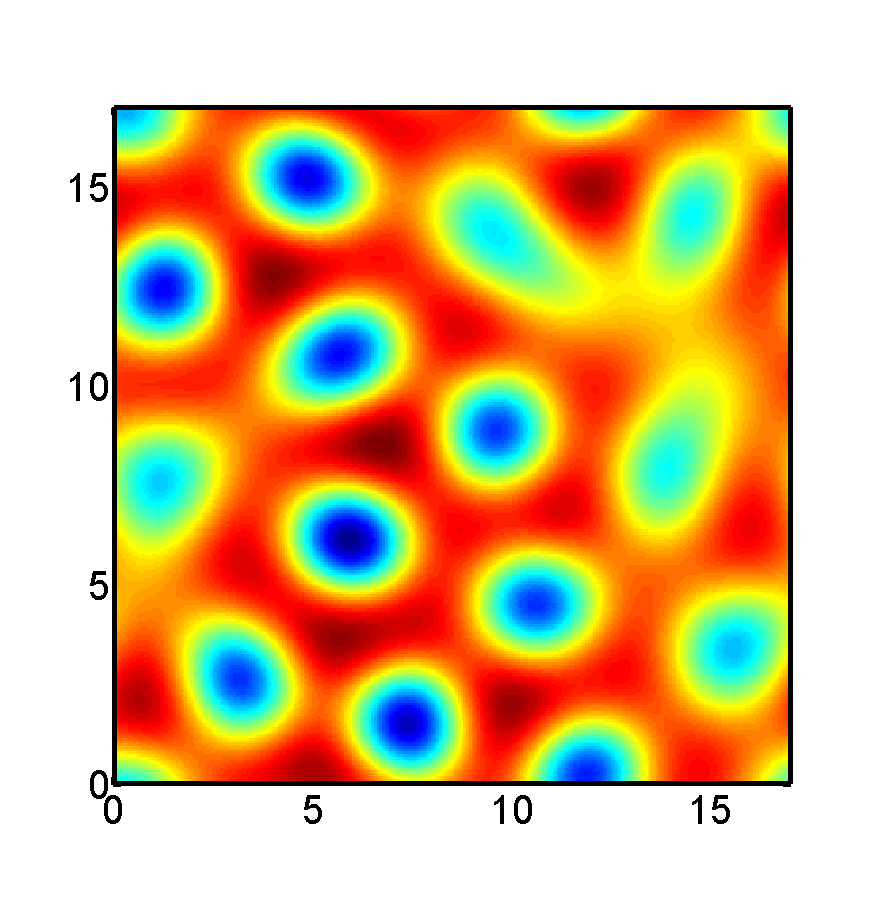
Above: A state which is far from the constant state (ie. O(1) distance away), but has energy O(10-5) lower. We adopt a global approach to compare these types of states.