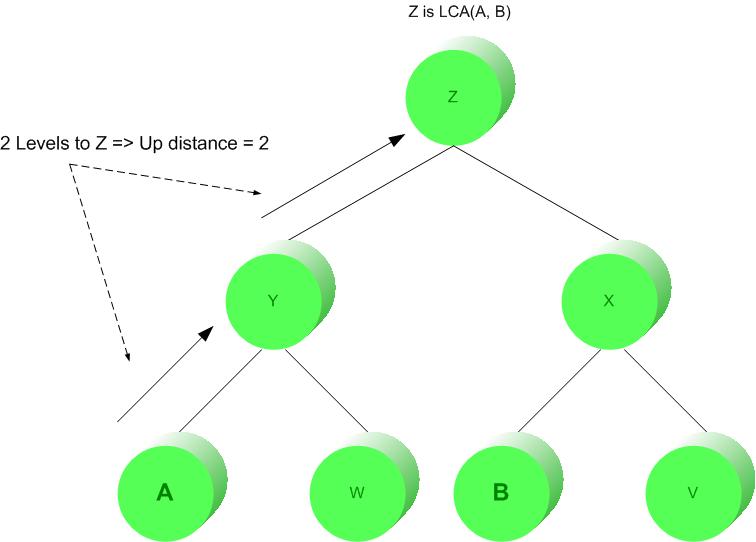
Figure 1: Up distance
Jason T. L. Wang
Bioinformatics Program
Department of Computer Science
New Jersey Institute
of Technology
wangj@njit.edu
Steven Regula
Department of Computer Science
New Jersey Institute of Technology
Dennis Shasha
Courant Institute of Mathematical Sciences
Department of Computer Science
New York University
Lei Hua
Department of Computer Science
New Jersey Institute of Technology
Rekha Patel
Department of Computer Science
New Jersey Institute of Technology
We describe an efficient method for evaluating closeness of tree matches when comparing a query tree P with a data tree D where both P and D are phylogenetic trees. The method computes the Updown distance between P and D.
The phylogenetic trees satisfy the following properties:
For more information and examples of computing the Updown distance of phylogenetic trees with this tool, see Example 1, Example 2, Example 3, or Example 4 and also some highlighted Special Cases.
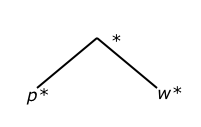
Before the Updown distance can be computed between a query and data tree, the calculation called "Up distance" must first be understood. Up distance between any node "A" and any node "B" is solved by counting the edges upwards in the tree from "A" to the lowest common ancestor of "A" and "B". This concept is demonstrated by Figure 1 below.

The formula for calculating the Updown distance between two trees, P and D, is:
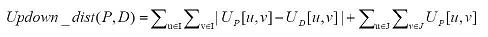
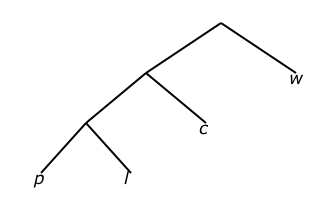
A key concept to successfully utilizing this formula is to generate Up distance matrices for all nodes to all nodes in both trees P and D. For example, consider the query tree P in (i) of Figure 3:
P in Newick format:
(((p,l),c),w);
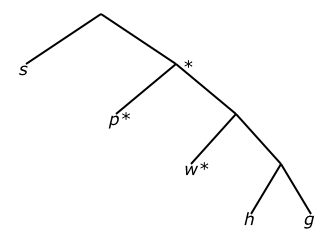
Before the Up distance matrix can be computed for data tree D, it should be reduced using the process described in the home page. Below in Figure 3 is the data tree D, before reduction, after being marked for reduction, and the finally reduced version.
D in Newick format:
(s,(p,(w,(h,g))));
 |
 |
 |
|
(i) |
(ii) |
(iii) |
Figure 3: (i) Query tree P, (ii) marked data tree D, and (iii) reduced data tree D*
Now that the data tree D has been calculated, we can create the Up distance matrices for both P and reduced data tree D*. These matrices are listed in Figures 4 and 5, respectively.
|
Pleo |
Lepto |
Cucur |
West | |
|
Pleo |
0 |
1 |
2 |
3 |
|
Lepto |
1 |
0 |
2 |
3 |
|
Cucur |
1 |
1 |
0 |
2 |
|
West |
1 |
1 |
1 |
0 |
Figure 4: The Up distance matrix for the query tree P
|
Pleo |
West | |
|
Pleo |
0 |
1 |
|
West |
1 |
0 |
Figure 5: The Up distance matrix for the reduced data tree D*
In what follows, we use D to represent D* for simplicity. The first part of the Updown distance formula involves the intersection of P and D, denoted as I (see Figure 6 below). For this part we calculate for all nodes u in I and for all nodes v in I, the Up distance from u to v in P minus the Up distance from u to v in the reduced data tree D.
![]()
Figure 6: First part of Updown distance computation
For this example that sum works out to be:
UpdistanceP(Pleo, West) - UpdistanceD(Pleo, West) = 3-1 =
2
+
UpdistanceP(West, Pleo) - UpdistanceD(West, Pleo) = 1-1 = 0
= 2
The second part of the Updown distance formula involves the subtraction of D from P, as shown in Figure 7.
![]()
Figure 7: Second part of Updown distance computation
This subtraction results in a node list J of all nodes in P that are not in D. Then for all nodes u in J and for all nodes v in J, the Up distance from u to v in P should be summed. For this example, using the Up distance matrix for P we obtain the following results:
(UpdistanceP(Lepto, Lepto) = 0)+
(UpdistanceP(Lepto, Cucur) =
2)+
(UpdistanceP(Cucur, Lepto) = 1)+
(UpdistanceP(Cucur, Cucur) = 0) = 3
Combining part 1 of the Updown distance
computation with part 2
yields an Updown distance of 2+3 = 5 for trees P and D.