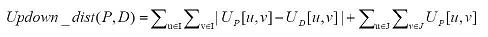
Equation 1
Jason T. L. Wang
Bioinformatics Program
Department of Computer Science
New Jersey Institute
of Technology
wangj@njit.edu
Steven Regula
Department of Computer Science
New Jersey Institute of Technology
Dennis Shasha
Courant Institute of Mathematical Sciences
Department of Computer Science
New York University
Lei Hua
Department of Computer Science
New Jersey Institute of Technology
Rekha Patel
Department of Computer Science
New Jersey Institute of Technology
We describe an efficient method for evaluating closeness of tree matches when comparing a query tree P with a data tree D where both P and D are phylogenetic trees. The method computes the Updown distance between P and D.
The phylogenetic trees satisfy the following properties:
For more information and examples of computing the Updown distance of phylogenetic trees with this tool, see Example 1, Example 2, Example 3, or Example 4 and also some highlighted Special Cases.
Under certain circumstances, the system may not be able to calculate Updown distance and instead will return a message describing the problem. Referring to the formula for Updown_dist(P,D) in Equation 1, such cases are described below.
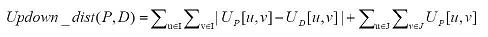
Equation 1
Case 1
Rule 1: If J has only one node, the node pair (u, v) is undefined, and hence the Updown_dist(P,D) is undefined.
If at any time, Updown_dist(P,D) is undefined (as would be the case if there was only one node in the intersection I or subtraction J) the system will return the following message:
Undefined
An example of how this can happen is as follows:
Imagine a query tree P with the following format: (a,b)c; and a data tree D (a,b);. In this case the intersection would have two nodes: "a" and "b", as well as only one node in J (V[P] - V[D]): c.
When J has only one node, the Updown_dist(P,D) is undefined.
Case 2
Rule 2: If J has zero nodes, there does not exist any (u, v) pair in J, and hence the second item in Equation 1 for calculating Updown_dist(P,D) is 0.
Case 3
Rule 3: If the intersection I has only one node, Updown_dist(P,D) is undefined.
Case 4
Rule 4: If the intersection I has zero nodes, the first item in the Updown distance formula is 0.
Rationale: The Updown distance is calculated from the query tree perspective. That's why we distinguish between a query tree and a data tree, instead of saying two general trees. If the intersection I has zero nodes, then J contains all nodes in the query tree. Under this circumstance, the Updown distance is totally dependent on the query tree, ignoring those nodes in the data tree. The more nodes the query tree has, the larger the distance.