Go to ECE489 Experiment | 1 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ECE Lab home
![]()
|
|
Go to ECE489 Experiment | 1 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ECE Lab home |
|
ECE 489 Communications Systems Laboratory
Experiment 2: Measurements on Noise
Introduction
The ultimate limitations on the performance of communication systems are due to noise. Thermal noise, which is caused by the random motion of electrons in resistors cannot be eliminated and must be considered by designers of communication systems. These thermal noise voltages are typically in the order of microvolts and are not noticed when working with voltages in the order of volts. At the input of communication receivers, however, where the received signal powers may be on the order of 10-12 watts, thermal noise power cannot be neglected. For this reason engineers working with communication systems should have some knowledge of the properties of noise.
Noise -A Tutorial
The thermal noise produced by a resistor has an rms value that is given by
|
|
(5.1) |
The variables appearing in the above equation are defined below
|
Variables in equation 5.1 |
|
|
T = Temperature in degrees Kelvin (°K) |
(5.2) |
|
k = Boltzmann's constant = 1.38 x 10-23 joules/°K |
(5.3) |
|
R = Resistance in Ohms |
(5.4) |
|
B = bandwidth in Hz over which the noise voltage is measured |
(5.5) |
As an example take a 100 kW resistor at a room temperature of 300°K. When measured with an ideal rms voltmeter having a bandwidth of 1 MHz, it would have a noise voltage of 20mV.
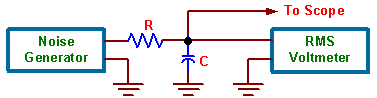 |
| Figure 5.1: Noise measurement setup |
The two properties of an electrical noise signal we are most interested in are:
1. How its power is distributed in the frequency domain, namely we would like to know its Power Special Density.
2. How its amplitude is distributed in a statistical sense, namely the probability density function of its amplitude.
The thermal noise we deal with in communication systems is closely modeled as White Gaussian Noise (WGN), which means that its power spectral density is uniform over a large frequency range and the probability density function of its amplitude is Gaussian. The noise generator we will use in this experiment has an output which approximates WGN over the frequency range 0 £ f ³ 500 kHz.
The relation between the power spectral density at the input and output of a linear system is given by
|
So ( f ) = Sin ( f ) | H( f )|2 |
(5.6) |
Power is related to the one sided spectral density S ( f ) by
|
|
(5.7) |
In this experiment we will not measure power, but rms voltage, which is more convenient to measure. Power is related to Vrms by
|
|
(5.8) |
THE EXPERIMENT
The experiment will attempt
to verify that the output of the noise generator has a constant power spectral
density ![]() over
a frequency range from DC to several hundred kilohertz. It should also familiarize
the student with the appearance of Gaussian noise when viewed on an oscilloscope.
over
a frequency range from DC to several hundred kilohertz. It should also familiarize
the student with the appearance of Gaussian noise when viewed on an oscilloscope.
Set up the circuit shown in figure 5.1. Choose R to be some convenient value such as 1 kW. Use 5 or 6 different values of C chosen such that the bandwidth of the RC lowpass filter varies from a few hundred hertz to a few hundred kilohertz.
For each value of C measure the rms voltage across the capacitor and observe it on the scope. Make rough sketches, showing height of peaks, for one value of C.
Plot
the
![]() as
a function of the bandwidth of the filter. Since the band- width will vary over
a range of a few thousand, as will
as
a function of the bandwidth of the filter. Since the band- width will vary over
a range of a few thousand, as will
![]() so a log-log plot would be desirable. From your plot determine
so a log-log plot would be desirable. From your plot determine ![]() for the generator .
for the generator .
In your report answer the following questions.
Use your communication systems book or any other communication systems book as a reference.
1. What is meant by the noise bandwidth of a filter? For the RC lowpass filter used in this experiment how are the 3 dB bandwidth and the noise bandwidth related ?
2. Why is
it necessary to use a "true rms meter" when measuring noise if you
are to obtain accurate results ?
3. How is the height of "fairly frequently seen"
peaks related to the rms value of a signal. (This is meant to be a rough approximation
as this term is not well defined. )
|
|
Go to ECE489 Experiment | 1 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ECE Lab home |
|