Go to ECE489 Experiment | 1 | 2 | 3 | 4 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ECE Lab home
![]()
|
|
Go to ECE489 Experiment | 1 | 2 | 3 | 4 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ECE Lab home |
|
ECE 489 Communications Systems Laboratory
Experiment 5: Amplitude Modulation
ACHIEVEMENTS: modeling of an amplitude modulated (AM) signal; method of setting and measuring the depth of modulation; waveforms and spectra; trapezoidal display.
PREREQUISITES: a knowledge of DSBSC generation. Thus completion of the experiment entitled DSBSC generation would be an advantage.
In the early days of wireless, communication was carried out by telegraphy, the radiated signal being an interrupted radio wave. Later, the amplitude of this wave was varied in sympathy with (modulated by) a speech message (rather than on/off by a telegraph key), and the message was recovered from the envelope of the received signal. The radio wave was called a 'carrier', since it was seen to carry the speech information with it. The process and the signal was called amplitude modulation, or 'AM' for short.
In the context of radio communication, near the end of the 2Oth century, few modulated signals contain a significant component at 'carrier' frequency. However, despite the fact that a carrier is not radiated. the need for such a signal at the transmitter (where the modulated signal is generated), and also at the receiver, remains fundamental to the modulation and demodulation process respectively. The use of the term 'carrier' to describe this signal has continued to the present day.
As distinct from radio communications, present day radio broadcasting transmissions do have a carrier. By transmitting this carrier the design of the demodulator, at the receiver, is greatly simplified, and this allows significant cost savings.
The most common method of AM generation uses a 'class C modulated amplifier'; such an amplifier is not available in the BASIC TIMS set of modules. It is well documented in text books. This is a 'high level' method of generation, in that the AM signal is generated at a power level ready for radiation. It is still in use in broadcasting stations around the world, ranging in powers from a few tens of watts to many megawatts.
Unfortunately, text books which describe the operation of the class C modulated amplifier tend to associate properties of this particular method of generation with those of AM, and AM generators, in general. This gives rise to many misconceptions. The worst of these is the belief that it is impossible to generate an AM signal with a depth of modulation exceeding 100% without giving rise to serious RF distortion.
You will see in this experiment, and in others to follow, that there is no problem in generating an AM signal with a depth of modulation exceeding 100%, and without any RF distortion whatsoever.
But we are getting ahead of ourselves, as we have not yet even defined what AM is !
The amplitude modulated signal is defined as:
| AM = E (1 + m·cosmt ) coswt | ( 1 ) |
| = A (1 + m·cosmt) · B coswt | ( 2 ) |
| = [ low frequency term a(t) ] x [ high frequency term c(t) ] | ( 3 ) |
Here:
'E' is the AM signal amplitude from eqn. ( 1 ). For modeling convenience eqn. ( 1 ) has been written into two parts in eqn. ( 2 ), where (A·B) = E.
'm' is a constant, which, as you will soon see, defines the 'depth of modulation'. Typically m < 1. Depth of modulation, expressed as a percentage, is 100.m. There is no inherent restriction upon the size of 'm' in eqn. (1). This point will be discussed later .
'm' and 'w' are angular frequencies in rad/s, where m / (2·p) is a low, or message frequency, say in the range 300 Hz to 3000 Hz; and w / (2.p) is a radio, or relatively high, 'carrier' frequency. In TIMS the carrier frequency is generally 100 kHz.
Notice that the term a ( t ) in eqn. (3) contains both a DC component and an AC component. As will be seen, it is the DC component which gives rise to the term at w -the 'carrier' -in the AM signal. The AC term 'm.cosmt' is generally thought of as the message, and is sometimes written as m ( t ). But strictly speaking, to be compatible with other mathematical derivations. the whole of the low frequency term a ( t ) should be considered the message.
Thus:
a ( t ) = DC + m ( t ) ( 4 )
Figure 1 below illustrates what the oscilloscope will show if displaying the AM signal.
|
|
|
Figure 1 -AM, with m = 1, as seen on the oscilloscope |
A block diagram representation of eq. ( 2 ) is shown in Figure 2 below.
|
|
| Figure 2: generation of equation 2 |
For the first part of the experiment you will model eq. (2) by the arrangement of Figure 2. The depth of modulation will be set to exactly 100% (m = 1). You will gain an appreciation of the meaning of 'depth of modulation' , and you will learn how to set other values of 'm " including cases where m > 1.
The signals in eq. (2) are expressed as voltages in the time domain. You will model them in two parts, as written in eq. (3).
100% amplitude modulation is defined as the condition when m = 1. Just what this means will soon become apparent. It requires that the amplitude of the DC (= A) part of a ( t ) is equal to the amplitude of the AC part (= A.m). This means that their ratio is unity at the output of the ADDER, which forces 'm' to a magnitude of exactly unity.
By aiming for a ratio of unity it is thus not necessary to know the absolute magnitude of A at all
The magnitude of 'm' can be measured directly from the AM display itself.
Thus
( 5 )
where p and Q are as defined in Figure 3.
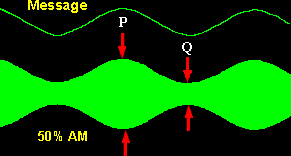 |
| Figure 3: the oscilloscope display for the case m = 0.5 |
Analysis shows that the sidebands of the AM, when derived from a message of frequency m rad/s, are located either side of the carrier frequency, spaced from it by m rad/s.
Figure 4: AM spectrum
You can see this by expanding eq. (2). The spectrum of an AM signal is illustrated in Figure 4 (for the case m = 0.75). The spectrum of the DSBSC alone was confirmed in the experiment entitled DSBSC generation. You can repeat this measurement for the AM signal.
As the analysis predicts. even when m > 1, there is no widening of the spectrum.
This assumes linear operation: that is, that there is no hardware overload.
Provided m £ 1 the envelope of the AM will always be a faithful copy of the message. For the generation method of Figure 2 the requirement is that:
The peak amplitude of the AC component must not exceed the magnitude of the DC, measured at the ADDER output
As an example of an AM signal derived from speech. Figure 5 shows a snap-shot of an AM signal, and separately the speech signal.
There are no amplitude scales shown, but you should be able to deduce the depth of modulation (the peak depth) by inspection.
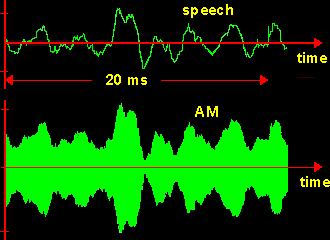 |
| Figure 5: AM derived from speech. |
There are many methods of generating AM, and this experiment explores only one of them. Another method, which introduces more variables into the model, is explored in the experiment entitled .Amplitude modulation -method 2, to be found in volume A2- Further & Advanced ,Analog Experiments.
It is strongly suggested that you examine your text book for other methods.
Practical circuitry is more likely to use a modulator, rather than the more idealized multiplier. These two terms are introduced in the Chapter of this Volume entitled Introduction to modeling with TIMS, in the section entitled multipliers and modulators.
The low frequency term a ( t )
To generate a voltage defined by eq. (2) you need first to generate the term a ( t ).
a ( t ) = A.(1 + m.cosmt) ( 6 )
Note that this is the addition of two parts, a DC term and an AC term. Each part may be of any convenient amplitude at the input to an ADDER.
The DC term comes from the VARIABLE DC module, and will be adjusted to the amplitude 'A' at the output of the ADDER.
The AC term m ( t ) will come from an AUDIO OSCILLATOR, and will be adjusted to the amplitude 'A·m' at the output of the ADDER.
The 100 kHz carrier c ( t ) comes from the MASTER SIGNALS module
c ( t ) = B.coswt ( 7 )
The block diagram of Figure 2, which models the AM equation, is shown modeled by TIMS in Figure 6 below.
|
|
| Figure 6: the TIMS model of the block diagram of Figure 2 |
To build the model
T1 First patch up according to Figure 6, but omit the input X and Y connections to the MULTIPLIER. Connect to the two oscilloscope channels using the SCOPE SELECTOR, as shown.
T2
Use the FREQUENCY COUNTER to set the AUDIO OSCILLATOR
to about 1 kHz.
T3
Switch the SCOPE SELECTOR to CH1-B, and look at the message
from the AUDIO OSCILLATOR. Adjust the oscilloscope
to display two or three periods of the sine wave in the top half of the screen.
Now start adjustments by setting up a ( t ), as defined by eqn. (4), and with m = 1
T4 Turn both g and G
fully anti-clockwise. This removes both the DC and the AC parts of the message from the output of the ADDER.
T5
Switch the scope selector to CH1-A. This is the ADDER
output. Switch the oscilloscope amplifier
to respond to DC if not already so set, and the sensitivity to about 0.5
volt/cm. Locate the trace on a convenient grid line towards the bottom of
the screen. Call this the zero reference grid line.
T6
Turn the front panel control on the VARIABLE DC module almost fully anti-
clockwise (not critical). This will provide an output voltage of about minus 2 volts. The ADDER will reverse its
polarity, and adjust its amplitude using the 'g'
, gain control.
T7
Whilst noting the oscilloscope reading on CH1-A,
rotate the gain 'g' of the
ADDER clockwise to adjust the DC term at the output of the
ADDER to exactly 2 cm above the previously set zero reference
line. This is 'A ' volts.
You have now set the magnitude of the DC part of the message to a known amount. This is about 1 volt, but exactly 2 cm, on the oscilloscope screen. You must now make the AC part of the message equal to this, so that the ratio Am/A will be unity. This is easy:
T8 Whilst watching the oscilloscope trace of CH1-A rotate the ADDER gain control
'G' clockwise. Superimposed on the DC output
from the ADDER will appear the message sinewave. Adjust the gain
G until the lower crests of the sinewave are EXACTLY coincident with
the previously selected zero reference grid line.
The sine wave will be centered exactly A volts above the previously-chosen zero reference, and so its amplitude is A.
Now the DC and AC, each at the ADDER output, are of exactly the same amplitude A. Thus:
A = A · m ( 8 )
and so:
m = 1 ( 9 )
You have now modeled A.(1 + m.cosmt), with m = 1. This is connected to one input of the MULTIPLIER, as required by eqn. (2).
T9 Connect the output of the
ADDER to input
X of the MULTIPLIER.
Make Sure the MULTIPLIER is switched to accept
DC.
Now prepare the carrier signal:
c ( t ) = B.coswt ( 10 )
T10 Connect a 100 kHz analog signal from the
MASTER SIGNALS module to input Y
of the MULTIPLIER
T11
Connect the output of the MULTIPLIER to the CH2-A
of the SCOPE SELECTOR. Adjust the oscilloscope to display the signal conveniently
on the screen.
Since each of the previous steps has been completed successfully, then at the MULTIPLIER output will be the 100% modulated AM signal. It will be displayed on CH2-A. It will look like Figure 1.
Notice the systematic manner in which the required outcome was achieved. Failure to achieve the last step could only indicate a faulty MULTIPLIER ?
It is now possible to check some theory
T12 Measure the peak-to-peak amplitude of the AM signal, with m
= 1, and
confirm that this magnitude is as predicted, knowing the signal levels into
the MULTIPLIER, and its 'k'
factor.
First note that the shape of the outline, or envelope. of the AM waveform (lower trace), is exactly that of the message waveform (upper trace). As mentioned earlier, the message includes a DC component, although this is often ignored or forgotten when making these comparisons.
You can shift the upper trace down so that it matches the envelope of the AM signal on the other trace. Now examine the effect of varying the magnitude of the parameter 'm'. This is done by varying the message amplitude with the ADDER gain control G.
for all values of 'm' less than that already set (m = 1), the envelope of the AM is the same shape as that of the message.
for values of m > 1 the envelope is NOT a copy of the message shape.
It is important to note that, for the condition m > 1:
it should not be considered that there is envelope distortion, since the resulting shape, whilst not that of the message, is the shape the theory predicts.
there need be no AM
signal distortion for this method of generation. Distortion of
the AM signal itself, if present, will be due to amplitude overload of the
hardware. But overload should not occur, with the levels previously recommended,
for moderate values of m > 1.
T13 Vary the ADDER gain G, and thus 'm' and confirm that
the envelope of the AM behaves as expected, including for values of
m > 1.
|
|
| Figure 7: the AM envelope for m < 1 and m > 1 |
T14 replace the AUDIO OSCILLATOR output with a speech signal available at the TRUNKS PANEL. How easy is it to set the ADDER gain G to occasionally reach, hut never exceed, 100% amplitude modulation ?
With the display method already examined, and with a sinusoidal message, it is easy to set the depth of modulation to any value of 'm'. This method is less convenient for other messages, especially speech.
The so-called trapezoidal display is a useful alternative for more complex messages. The patching arrangement for obtaining this type of display is illustrated in Figure 8 below. and will now be examined.
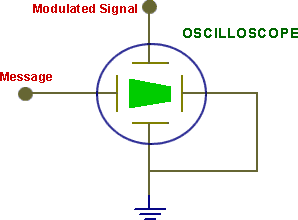 |
| Figure 8: the arrangement for producing the TRAPEZOID |
T15 Patch up the arrangement of figure 8. Note that the oscilloscope will have to be switched to the 'X- Y' mode,. the internal sweep circuits are not required.
T16
With a sine wave message show that, as m is increased from zero,
the display takes on the shape of a TRAPEZOID (Figure 9).
T17
Show that, for m =
1, the TRAPEZOID degenerates into a
TRIANGLE
T18
Show that, for m >
1, the TRAPEZOID extends beyond the TRIANGLE, into the dotted region
as illustrated in Figure 9
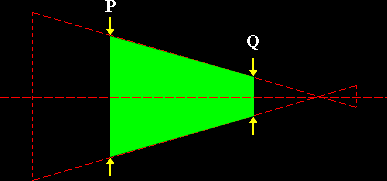 |
| Figure 9: the AM trapezoid for m = .5. The trapezoid extends into the dotted section as m is increased to 1.2 (120%). |
So here is another way of setting m = 1. But this was for a sinewave message, where you already have a reliable method. The advantage of the trapezoid technique is that it is especially useful when the message is other than a sine wave -say speech.
T19
Use speech as the message, and show that this also generates a TRAPEZOID,
and that setting the message amplitude so that the depth of modulation reaches
unity on peaks (a TRIANGLE) is especially easy to do.
Practical
note: if the outline of the
trapezoid is not made up of straight-line sections then this is a good indicator
of some form of distortion. For m < 1 it could be phase distortion, but for
m > 1 it could also be overload distortion. Phase distortion is not likely
with TIMS, but in practice it can be caused by (electrically) long leads to
the oscilloscope, especially at higher carrier frequencies.
Q1
There is no difficulty in relating the formula of eqn. (5) to the
waveforms of Figure 7 for values of 'm' less than unity.
But the formula is also valid for m >
1, provided the magnitudes P
and Q are interpreted correctly. By varying 'm' and
watching the waveform, can you see how P and Q are defined for m
>
1 ?
Q2
Explain how the arrangement of Figure 8 generates the TRAPEZOID of
Figure 9, and the TRIANGLE as a special case.
Q3
Derive eqn.(5), which relates the magnitude of the parameter
'm' to the peak-to-peak and trough-to-trough amplitudes of the AM signal.
Q4
If the AC/DC switch on the MULTIPLIER front panel is switched to AC what
will the output of the model of Figure 6 become ?
Q5
An AM signal, depth of modulation 100%.from a single tone message, has a
peak-to-peak amplitude of 4 volts. What would an RMS voltmeter read if
connected to this signal ? You can check your answer if you have a WIDEBAND
TRUE RMS METER module.
Q6 In Task T6, when modeling AM, what difference would there have been to the AM from the MULTIPLIER if the opposite polarity (+ ve) had been taken from the VARIABLE DC module ?
|
|
Go to ECE489 Experiment | 1 | 2 | 3 | 4 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ECE Lab home |
|